Sommario: 12.1 Introduzione – 12.2 Inquadramento tecnico – 12.3 I “nuovi” vettori energetici – 12.4 Analisi e selezione del modello di rilascio a getto – 12.5 Validazione del modello – 12.6 Alcune ATEX-annotazioni – 12.7 Esempi di calcolo
Abstract: Il Capitolo si propone di introdurre la tematica degli “ATEX energy carrier”, di validare una modello di calcolo per la dispersione di fluidi criogenici e supercritici derivato dalla Norma NFPA 2:2023 e di illustrare l’applicazione del metodo attraverso lo svolgimento di specifici esempi di calcolo.
«Tutti i modelli sono sbagliati ma alcuni sono utili.»
George Edward Pelham Box
12.1 Introduzione
Viviamo un’epoca di grandi cambiamenti e la transizione energetica è senza dubbio uno tra i più importanti. Entro la seconda metà di questo secolo, infatti, il settore energetico dovrà essere convertito da base fossile a “zero-carbon”. Tale scelta nasce dalla necessità di ridurre l’inarrestabile crescita nella produzione ed immissione in atmosfera di anidride carbonica, il principale gas correlato ai grandi cambiamenti climatici in atto. In particolare, l’obiettivo dell’accordo di Parigi consiste nella riduzione della CO2 antropogenica a livelli tali da limitare il riscaldamento globale entro i 2 °C rispetto alla temperatura media preindustriale.
L’ottenimento dei risultati che la comunità internazionale si è data passerà necessariamente da un complessivo ridisegno dell’utilizzo dei gas vettori energetici, i cosiddetti “energy carrier”: gas naturale liquefatto (LNG) e idrogeno su tutti.
Tali gas, ad oggi, vengono utilizzati per scopi energetici in forme termodinamiche particolari: l’LNG allo stato criogenico (a pressione ambiente questo significa una temperatura del fluido di circa –161 °C) mentre l’idrogeno in forma supercritica (le applicazioni automotive prevedono pressioni di stoccaggio di 700 bar in auto e 1000 bar al distributore).
Queste particolari condizioni di fornitura necessitano, dunque, di un approfondimento tecnico rispetto alle tematiche connesse alle atmosfere esplosive ATEX.
12.2 Inquadramento tecnico
La disciplina per il calcolo degli effetti prevedibili di un’esplosione ATEX è da sempre caratterizzata da almeno tre grandi tipologie di modelli:
-
le trattazioni dedicate al calcolo delle portate di emissione, ad esempio derivanti da pozza in fase di evaporazione oppure causata dal rilascio di un gas in pressione oppure (ancora) dovuta all’emissione di un fluido bifase, ecc.;
-
i modelli destinati al calcolo della dispersione nell’ambiente. In questo ambito sono rinvenibili relazioni sia di campo vicino (entro qualche metro dalla sorgente) sia di campo lontano (dell’ordine dei km nel caso di sostanze nocive e/o tossiche);
-
e, infine, le simulazioni volte a calcolare gli effetti dei rilasci innescati (incendio ed esplosione): calcolo della potenza termica di un jetfire anziché gli effetti di sovrappressione derivanti da un’esplosione non confinata.
A questa modellistica, di derivazione ingegneristica, si è (relativamente) recentemente aggiunta quella di tipo fluidodinamico con integrazione numerica delle equazioni di Navier-Stokes: la cosiddetta fluidodinamica computazionale (CFD).
Per gli scopi collegati alla classificazione delle zone ATEX solo una parte della notevole mole di studi esposta risulta, tuttavia, utile e pragmaticamente applicabile. Se è infatti vero che un modello CFD 3D lascia stupefatti per la quantità di informazioni potenzialmente disponibili, per gli scopi finalizzati alla determinazione dell’ampiezza delle zone a rischio di esplosione ci si può servire dei cosiddetti “modelli integrali” (Ivings et al., 2007) che presentano una serie di equazioni contenenti semplici e intuitive descrizioni della dinamica di dispersione in atmosfera. Peraltro, la modellazione integrale calcola la grande parte dei parametri la cui conoscenza risulta indispensabile al decisore tecnico per l’apprestamento delle misure di prevenzione e protezione.
In questo Capitolo ci vogliamo concentrare sull’evoluzione dei modelli integrali di campo vicino dedicati alla quantificazione della relazione, tipicamente iperbolica, tra la concentrazione di infiammabile e la distanza dalla sorgente di emissione ATEX in pressione. Relazioni matematiche, cioè, valide nel campo di velocità governato dalla quantità di moto dov’è presente la progressiva miscelazione in aria della miscela infiammabile1. Per semplicità considereremo l’insieme dei modelli sottoespansi che hanno, cioè, una pressione di emissione superiore a circa 1,8-1,9 bar (assoluti) e che raggiungono, conseguentemente, velocità soniche in corrispondenza del bordo di emissione.
La necessità di una “nuova taratura” dei modelli ATEX nel caso degli energy carrier deriva dalla messe di studi che, nell’ultimo decennio, hanno avuto come obiettivo l’approfondimento sperimentale delle dinamiche di emissione e dispersione dell’idrogeno. Le evidenze empiriche, per certi versi sorprendenti, hanno costretto a rivedere i modelli prevalentemente fondati su esperimenti con il gas naturale svolti a metà degli anni ‘80. Ci si propone, dunque, di:
-
proporre un modello di dispersione che possa essere utilizzato, con sicurezza, in tutti i contesti di rilascio ATEX (energy carrier e non);
-
validare il modello confrontandolo, nei risultati, sia con i più recenti studi basati sull’idrogeno che con le storiche evidenze sperimentali connesse al gas naturale e all’etilene2;
-
confrontare tale modellazione con i più affidabili software ora disponibili per le simulazioni di rilascio (cd. “Benchmark”). In questo caso le sostanze coinvolte saranno l’idrogeno e il metano;
-
proporre un esempio di calcolo che consenta di familiarizzare con tale nuova metodica di calcolo.
12.3 I “nuovi” vettori energetici
La transizione energetica richiede l’utilizzo di nuovi vettori energetici i quali, a dire il vero, proprio “nuovi” non sono. Discutiamo, in particolare, di idrogeno, gas naturale liquefatto (LNG) e ammoniaca. Tali sostanze risultano spesso presenti in ambito industriale, oil&gas, chimico, farmaceutico, ecc. La grande differenza rispetto all’utilizzo che se ne faceva fino a pochi anni fa è relativa al quadro di contesto. I parametri operativi sono differenti (temperature e pressioni) e il perimetro di utilizzo è differente: prima, all’interno di stabilimenti, tali sostanze erano utilizzate in contesti controllati da personale specializzato mentre ora avranno una progressiva diffusione di massa all’esterno di contesti industrializzati. I dettagli dei parametri termodinamici e di infiammabili delle tre sostanze sono di seguito riportati.
Tabella 12.1 – Parametri termodinamici e di infiammabilità di idrogeno, ammoniaca e LNG
| Proprietà | H2 | NH3 | LNG |
|---|---|---|---|
| Caratteristiche di dispersione | Galleggiamento | Gas denso se criogenico Galleggiamento a condizioni atmosferiche |
Gas denso se criogenico Galleggiamento a condizioni atmosferiche |
| Pericoli | Estremamente infiammabile Gas compresso |
Infiammabile Gas liquefatto Tossico se inalato Ustioni alla pelle e agli occhi Molto tossico per la vita acquatica |
Estremamente infiammabile Gas liquefatto |
| Limiti di infiammabilità | 4 ÷ 77% | 15 ÷ 33,6% | 4,4 ÷ 17% |
| AIT | 560 °C [T1] | 630 °C [T1] | 600 °C [T1] |
| Velocità di combustione laminare | 3,25 m/s | 0,1 m/s | 0,45 m/s |
| Effetto Joule-Thompson | Negativo | Positivo | Positivo |
| Coefficiente di diffusione | 0,75 cm2/s | 0,19 cm2/s | 0,22 cm2/s |
| MIE | 0,016 mJ [IIC] 0,0012 mJ (in O2) |
680 mJ [IIA] | 0,21 mJ [IIA] 0,0027 mJ (in O2) |
Pur non essendo il focus di questo manuale, si vogliono di seguito brevemente fornire alcune caratteristiche dei gas carrier.
12.3.1 Idrogeno
L’idrogeno è ormai universalmente considerato il gas di approdo della fase di transizione energetica. I motivi posti a fondamento della precedente affermazione sono sinteticamente i seguenti:
-
è versatile;
-
è efficiente, soprattutto se accoppiato a pile a combustibile;
-
ha un basso impatto ecologico, cd “zero emissions” (esiste tuttavia, se combusto, il tema degli ossidi di azoto);
-
può essere prodotto direttamente da fonte rinnovabile;
-
si presta ad essere miscelato al gas naturale in percentuali di circa 10% sfruttando le infrastrutture esistenti3;
-
La produzione di CO2 non è tuttavia azzerata se l’H2 è di tipo grigio o blu.
12.3.2 Gas Naturale Liquefatto (GNL/LNG)
L’LNG, pur non essendo certamente il vettore energetico di approdo del percorso che porterà alla progressiva decarbonizzazione energetica, rappresenta per il nostro paese una risorsa insostituibile in fase di transizione tenendo soprattutto il mix energetico italiano. È un gas ritenuto di transizione perché, pur emettendo CO2 in fase di combustione, ne emette meno degli idrocarburi con i quali si confronta. Quindi:
-
emette 365 kg/MWh di CO2 (il carbone 900 kg/MWh, il petrolio 565 kg/MWh);
-
esiste in Italia un’infrastruttura di trasporto tecnologicamente affidabile e collaudata;
-
l’Italia possiede stoccaggi di gas naturale pari al 17% dell’intera quantità stoccabile in UE (ed è seconda solo alla Germania);
-
è tecnologicamente maturo per un suo utilizzo su gomma (un litro di LNG genera 600 litri di NG a condizioni ambiente).
12.3.3 Ammoniaca
La produzione di ammoniaca rinnovabile apre un ampio ventaglio di utilizzi poiché:
-
ha nove volte la densità energetica delle batterie a ioni di litio;
-
ha tre volte l’energia dell’idrogeno compresso ad alta pressione;
-
crea un vettore energetico «carbon-free»;
È peraltro un buon combustibile alternativo dato che le infrastrutture di produzione e distribuzione sono già mature a scale rilevanti.
Un grande aspetto a sfavore è connesso alla sua tossicità: da sempre si cerca di minimizzarne le quantità presenti negli stoccaggi in impianti a rischio di incidente rilevante.
12.4 Analisi e selezione del modello di rilascio a getto
Come anticipato ad inizio Capitolo, alla luce delle problematiche ATEX introdotte dai nuovi carrier energetici ci si propone di individuare un modello di dispersione che possieda le seguenti caratteristiche:
-
approssimare il comportamento dei gas reali;
-
simulare l’emissione e la dispersione di gas criogenici (e quindi con temperatura del contenimento in pressione molto differente dalla temperatura dell’ambiente di rilascio);
-
modellizzare il comportamento di gas sottoespansi in fase di dispersione in aria attraverso il calcolo dello pseudo diametro di emissione (approfondiremo in seguito tale aspetto);
-
assumere che tra sezione di emissione reale e lo pseudo diametro si conservi sia la massa sia la quantità di moto;
-
consentire una semplice implementazione del modello su foglio di calcolo.
La selezione, svolta in base alla letteratura scientifica e tecnica riportata in bibliografia (filtrata attraverso i cinque criteri ora accennati), ci ha indirizzato alla sintesi presentata nell’allegato E.2.2, NFPA 2:2023. Tale modello verrà ora approfonditamente descritto utilizzando la medesima simbologia presente nello standard statunitense.
La prima versione della modellazione matematica contenuta in NFPA 2:2023 venne presentata da Birch et al. nel 1987 nel seguente paper (226 citazioni alla data pubblicazione del presente Manuale):
-
Birch, Hughes, Swaffield. “Velocity Decay of High Pressure Jets”. Combustion Science and Technology 52 (1987), 161-171.
Una semplificazione del modello, con l’eliminazione del coefficiente di rilascio Cd, venne successivamente elaborata da Houf et al. nel 2007 (160 citazioni alla data di pubblicazione del presente Manuale):
-
Houf, Schefer. “Predicting radiative heat fluxes and flammability envelopes from unintended releases of hydrogen”. International Journal of Hydrogen Energy 32.1 (2007): 136-151.
Il concetto chiave contenuto nella sintesi che ora andremo a presentare è riassumibile nei seguenti punti base:
-
le emissioni di gas compressi a pressione superiore a quella critica (1,7 ÷ 1,9 bar) generano, in corrispondenza del foro di scarico/guasto, una velocità pari a quella del suono nelle condizioni di pressione e temperatura ivi presenti;
-
il flusso di gas, in queste condizioni, diviene «soffocato» (“chocked”) non essendo più in grado di aumentare la propria velocità in presenza di incrementi della pressione di alimento;
-
tali condizioni di anomalia termodinamica producono, in corrispondenza del bordo di emissione, un flusso sottoespanso metastabile;
-
il fluido, successivamente all’uscita dal bordo fisico di contenimento, produrrà successive onde d’urto necessarie a raggiungere l’equilibrio termodinamico con l’ambiente esterno.
Fisicamente, quindi, il rilascio a getto con successivo, progressivo impoverimento della miscela infiammabile avrà inizio a partire dal bordo finale dell’espansione: tale limite viene chiamato pseudo-diametro, pseudo-sorgente oppure diametro fittizio (cfr. Figura 12.1).
Figura 12.1 – Pseudo-diametro derivante dall’emissione di H2 a varie pressioni da un foro avente diametro d = 1 mm. Si noti il progressivo incremento della dimensione all’aumentare della pressione di alimento
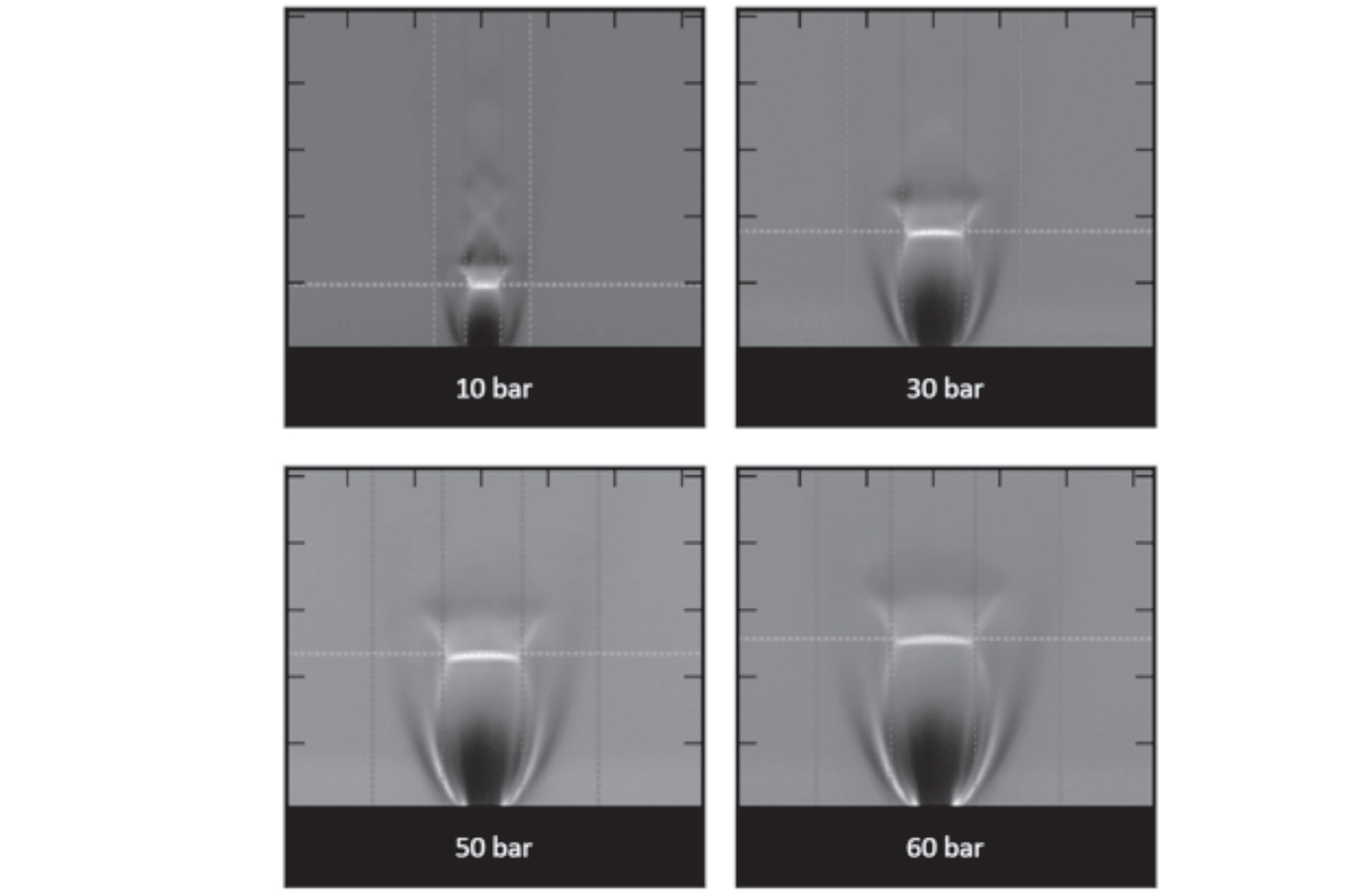
Fonte: Hecht et al., 2015
Tale modellazione risulta altresì presente nella Norma tecnica di classificazione CEI EN IEC 60079-10-1:2021, come appare evidente dalla “Figure C.2” dello standard. In essa viene specificato che il “ds” è il diametro della pseudo-sorgente, cioè il diametro trasversale del getto in corrispondenza della sezione a valle della quale le condizioni diventano isobare e a pressione atmosferica.
Figura 12.2 – Indicazione dello pseudo-diametro
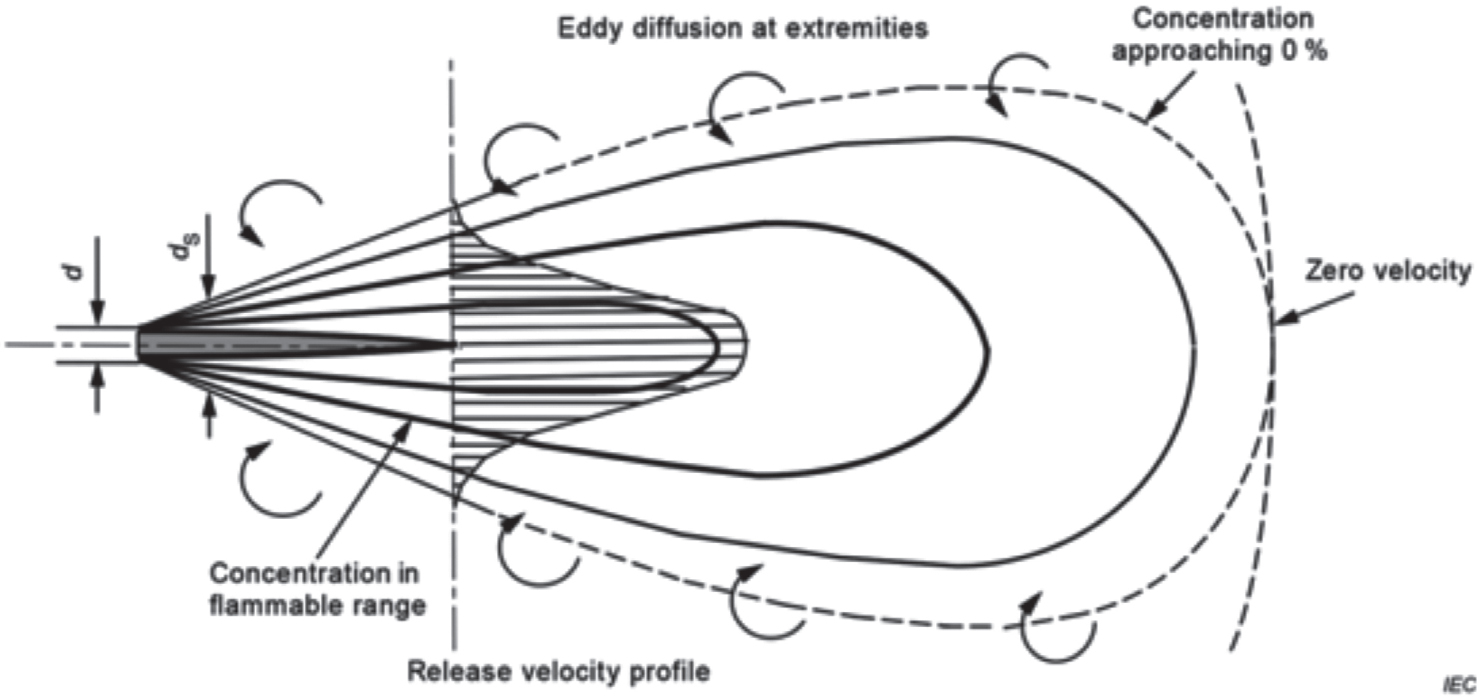
Fonte: Allegato C, CEI EN IEC 60079-10-1:2021
Il quadro analitico di fondo nel quale è iscritta la relazione iperbolica che lega la distanza dalla sorgente di emissione (dz) al limite inferiore di infiammabilità (LFL) del gas rilasciato è sintetizzabile nello schema di seguito riportato (adottando la notazione contenuta in NFPA 2:2023).
Figura 12.3 – Schema di rilascio sottoespanso secondo la notazione presente in NFPA 2:2023
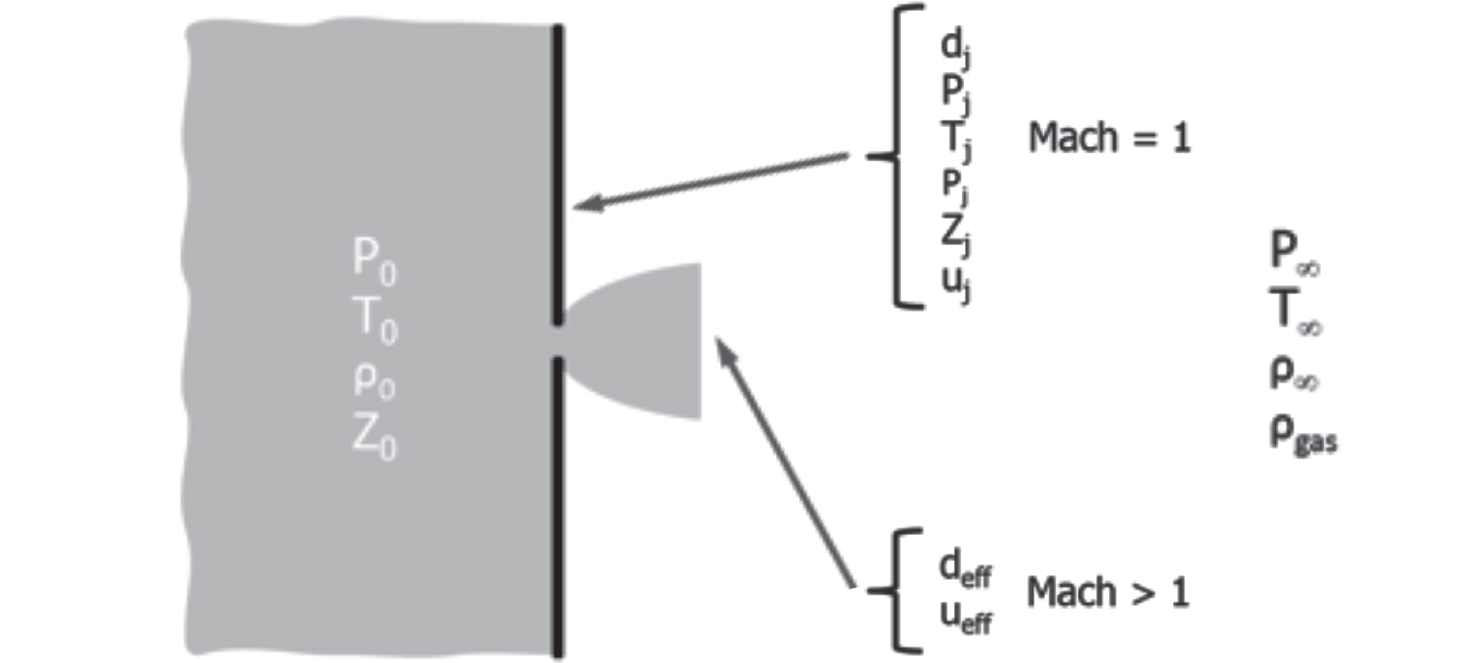
In particolare, l’ampiezza dello pseudo-diametro (deff) si calcola assumendo la costanza, tra foro reale e sorgente fittizia, della portata in massa e della quantità di moto del getto di rilascio. Si ha, quindi:

dove:
| dj | è il diametro reale di rilascio |
| Cd | è il coefficiente di emissione |
| ρj | è la densità reale del fluido nel bordo di uscita |
| ρgas | è la densità del gas a condizioni atmosferiche |
| uj | è la velocità del fluido nel bordo di uscita |
| ueff | è la velocità del fluido in corrispondenza dello pseudo-diametro |
A solo titolo d’esempio, nel caso di un rilascio a 200 bar il metano espanderà il proprio diametro fittizio di circa 11 volte mentre l’idrogeno non supererà il fattore 8,5. Al decrescere della pressione, com’è intuibile, diminuirà (per ogni gas) il rapporto deff/dj.
Una volta calcolato lo pseudo-diametro sarà possibile la determinazione della distanza in corrispondenza della quale la dispersione “leggerà” un dato valore di concentrazione (nel caso in esame assumiamo rappresentativo l’LFL). Si ottiene:

dove:
| k | è la costante di trasporto |
| ρ∞ | è la densità dell’aria in condizioni atmosferiche |
12.5 Validazione del modello
Il modello di calcolo verrà ora testato utilizzando evidenze sperimentali ad alta affidabilità, la prima delle quali è riferibile al gas naturale [Birch et al., 1984; Birch et al., 1987]. Il confronto, in particolare, ha come oggetto la relazione distanza-concentrazione nel caso di un’emissione avente le seguenti caratteristiche4:
-
Gas Naturale (M = 17,3 kg/kmol)
-
dj = 2,7 mm
-
P0 = 46 bar
Adottando una costante di trasporto (k) pari a 5,4 (come consigliato da Birch nel 1987) si ottiene il seguente grafico riportato in Figura 12.4.
Figura 12.4 – Confronto tra dati sperimentali e modello NFPA 2:2023, Gas Naturale
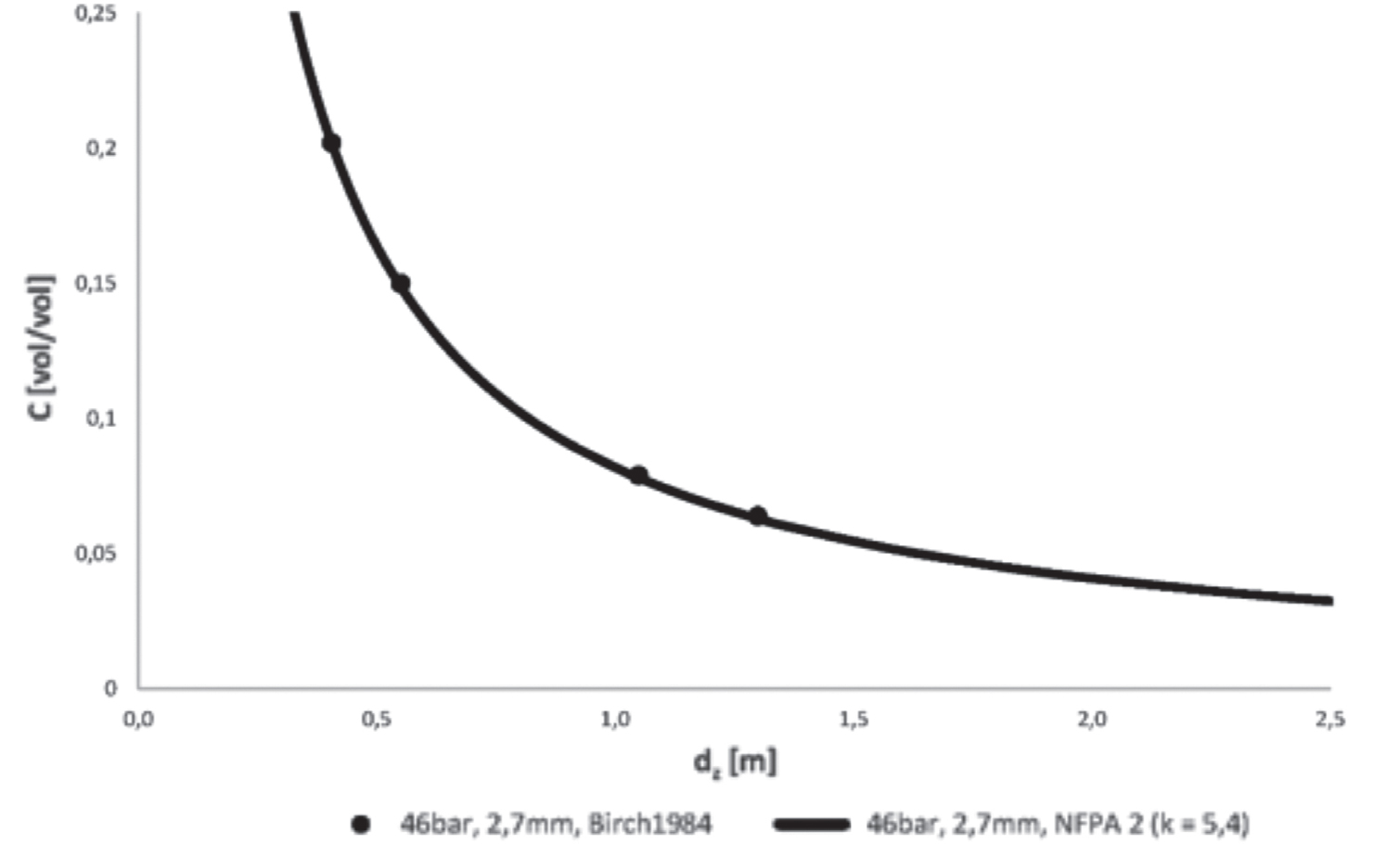
Fonte: Birch et al., 1984; Birch et al., 1987
Si nota un eccellente accordo tra le previsioni del modello e i dati sperimentali. Come previsto da Birch, quindi, la costante k = 5,4 è la giusta taratura della modellazione matematica nel caso del gas naturale.
Passiamo ora alla verifica del medesimo modello in condizioni differenti sia in termini di parametri di emissione che di gas di confronto. Lo studio è molto più recente [Han et al., 2013]:
-
Idrogeno (M = 2,016 kg/kmol)
-
dj = 0,7 mm
-
P0 = 400 bar
Il grafico di sintesi è appresso riportato nella Figura 12.5.
Figura 12.5 – Confronto tra dati sperimentali e modello NFPA 2:2023, Idrogeno
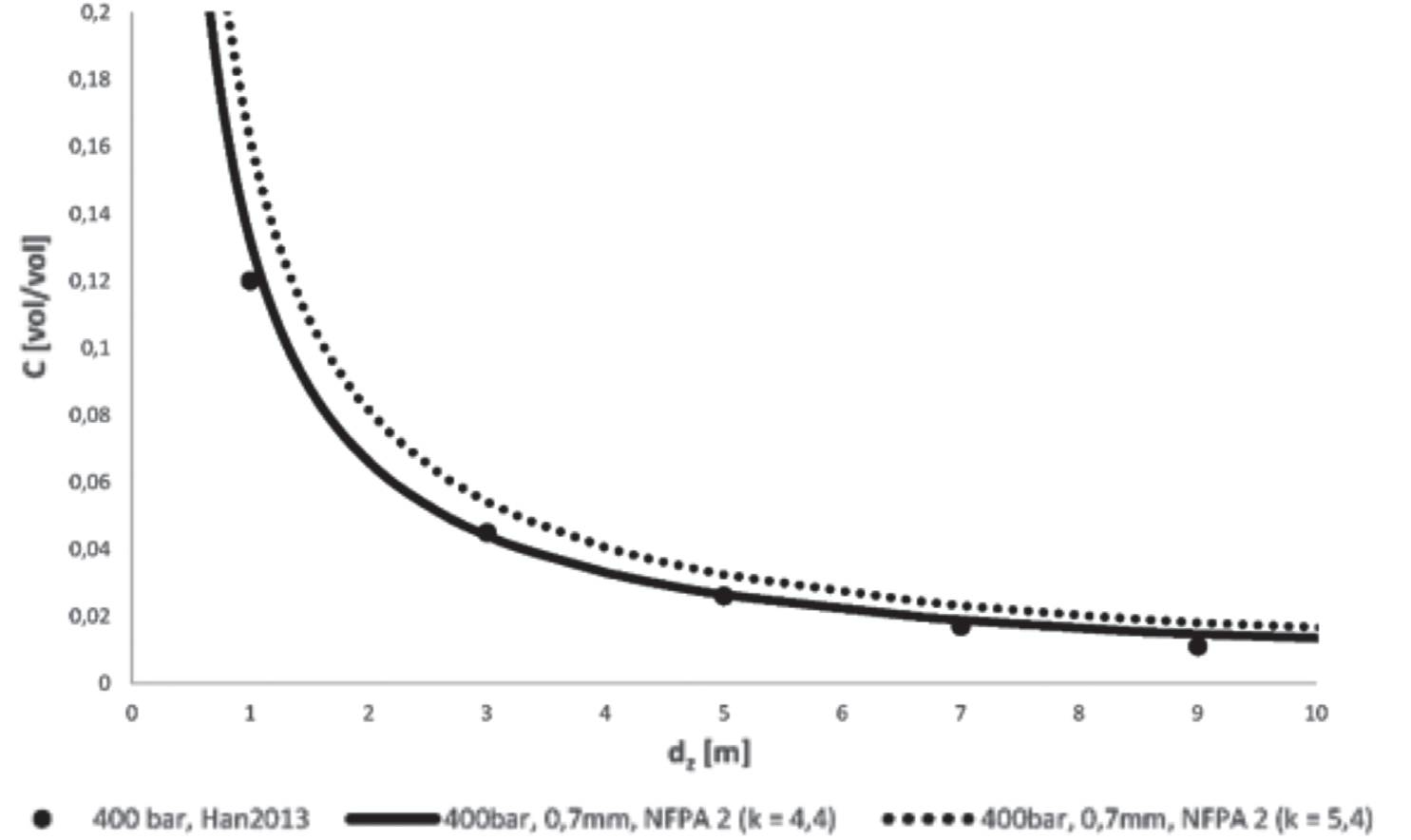
Han et al., 2013
A differenza del confronto precedente, in questo caso l’adozione del coefficiente k suggerito da Birch porta ad una decisa sovrastima della distanza correlata alla concentrazione. La sovrapposizione dei dati al modello si ottiene modificando il valore della costante di trasporto (k = 4,4). A titolo d’esempio, nel caso di concentrazioni di riferimento del 2% di H2 la differenza tra la distanza “esatta” (k = 4,4; dz = 6,6 m) e quella approssimata (k = 5,4; dz = 8,1 m) porta ad una sovrastima dell’ordine del 20%. Inoltre, facendo il raffronto con la metodologia TNO-Yellow Book, si ottiene, nelle medesime condizioni, un dz = 10,3 m (oltre il 50% superiore alla soluzione “esatta”). Nel caso di idrogeno supercritico alle pressioni tipiche dell’automotive (700-1000 bar) questo potrebbe tradursi nella possibilità, o meno, di poter dar corso ad una progettazione impiantistica di rilievo5.
Alla luce delle evidenze appena esposte, appare credibile che il coefficiente di trasporto (k) non sia indipendente dalla tipologia dei gas ma, al contrario, risulti connesso. Ipotizziamo, preliminarmente, che tale legame si esplichi in forma lineare al variare della massa molare. Due parametri già li abbiamo individuati:
-
Gas Naturale, M = 17,3 kg/kmol, k = 5,4
-
Idrogeno, M = 2,016 kg/kmol, k = 4,4
Testiamo ora tale ipotesi di variabilità nel caso di un rilascio di etilene. Lo studio al quale facciamo riferimento, già citato, è quello di Birch et al. del 1984. I parametri di emissione sono, in questo caso, i seguenti:
-
Etilene (M = 28,053 kg/kmol)
-
dj = 2,7 mm
-
P0 = 8 bar
Adottando la relazione di proporzionalità lineare appena definita tra la costante di trasporto (k) e la massa molare (M) si ottiene, nel caso dell’etilene, un valore di k pari a circa 6,1. La sintesi tra modello ed esperimento è quindi condensato nella seguente iperbole.
Figura 12.6 – Confronto tra dati sperimentali e modello NFPA 2:2023, Etilene
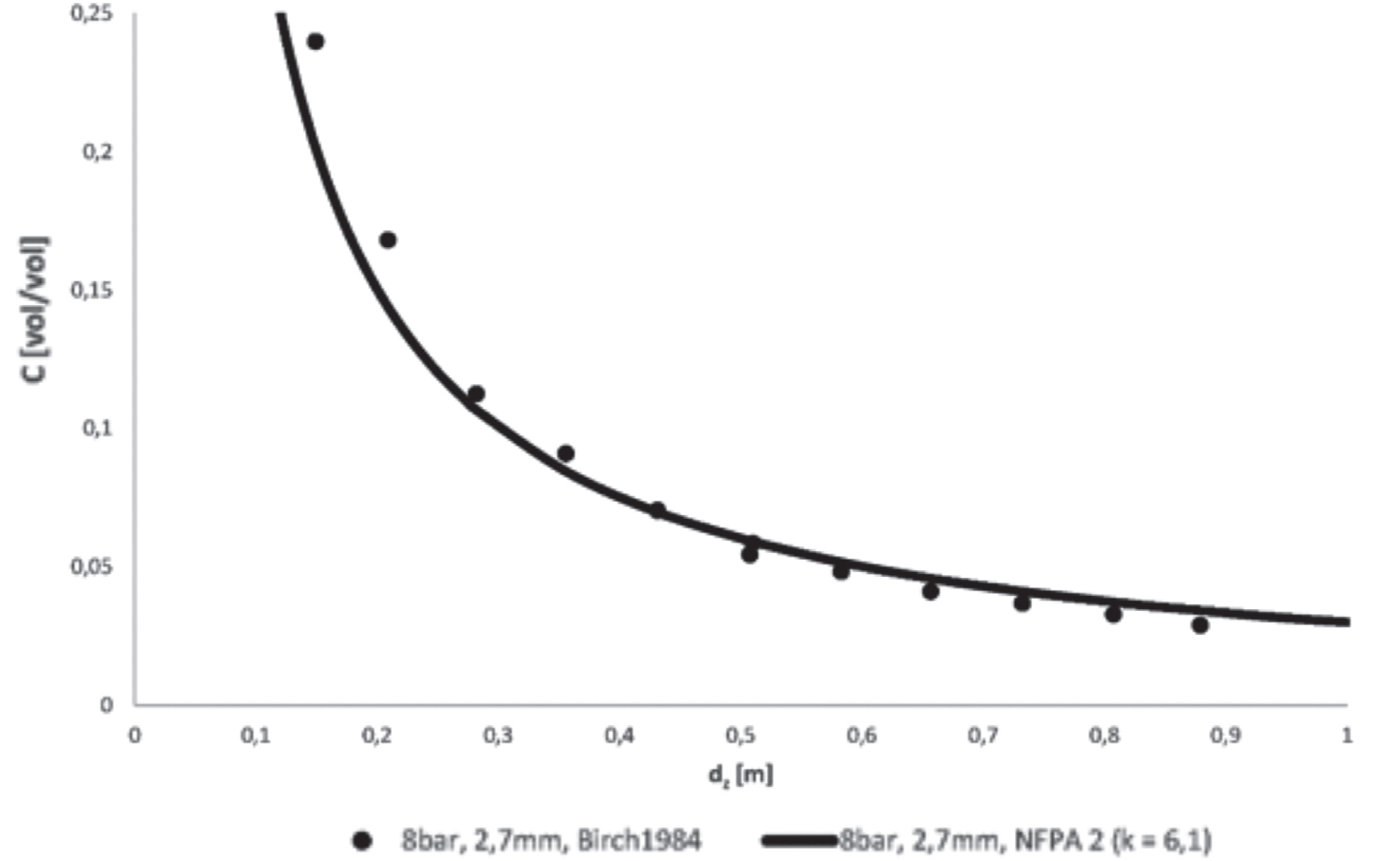
Birch et al., 1984
Appare evidente, anche in questo caso, il buon accordo tra la parte sperimentale ed il modello matematico di dispersione presente in NFPA 2:2023 (modificato nella parte di adozione del coefficiente “k”).
Passiamo ora alla verifica/benchmark delle previsioni del modello NFPA 2:2023 rispetto ai risultati forniti dai più diffusi e/o affidabili software ingegneristici reperibili alla data di redazione del presente contributo. Il riferimento, in particolare, è ai seguenti:
-
DNV-Phast, Vessel Leak (Build: 20230522.2)
-
GEXCON-Effects (Version: 12.1.0 “Victor”)
-
SANDIA-HyRAM+ (Version: 5.0)
Il range dei parametri di emissione testati è il seguente:
-
Idrogeno (M = 2,016 kg/kmol)
-
dj = 1,784 mm (S = 2,5 mm2)
-
P = 5 – 700 bar
-
k = 4,4
Si ottiene il seguente diagramma di sintesi nel quale è evidente la limitatissima dispersione dei risultati, sia tra i vari software che tra i software presi complessivamente e il modello NFPA 2:2023 modificato con k = 4,4. Si nota una sorprendente precisione nelle previsioni, probabilmente dettata dal particolare approfondimento sperimentale svolto, negli ultimi anni, sull’idrogeno.
Figura 12.7 – Benchmark tra software e modello NFPA 2:2023, Idrogeno, d = 1,784 mm, P = 5-700 bar
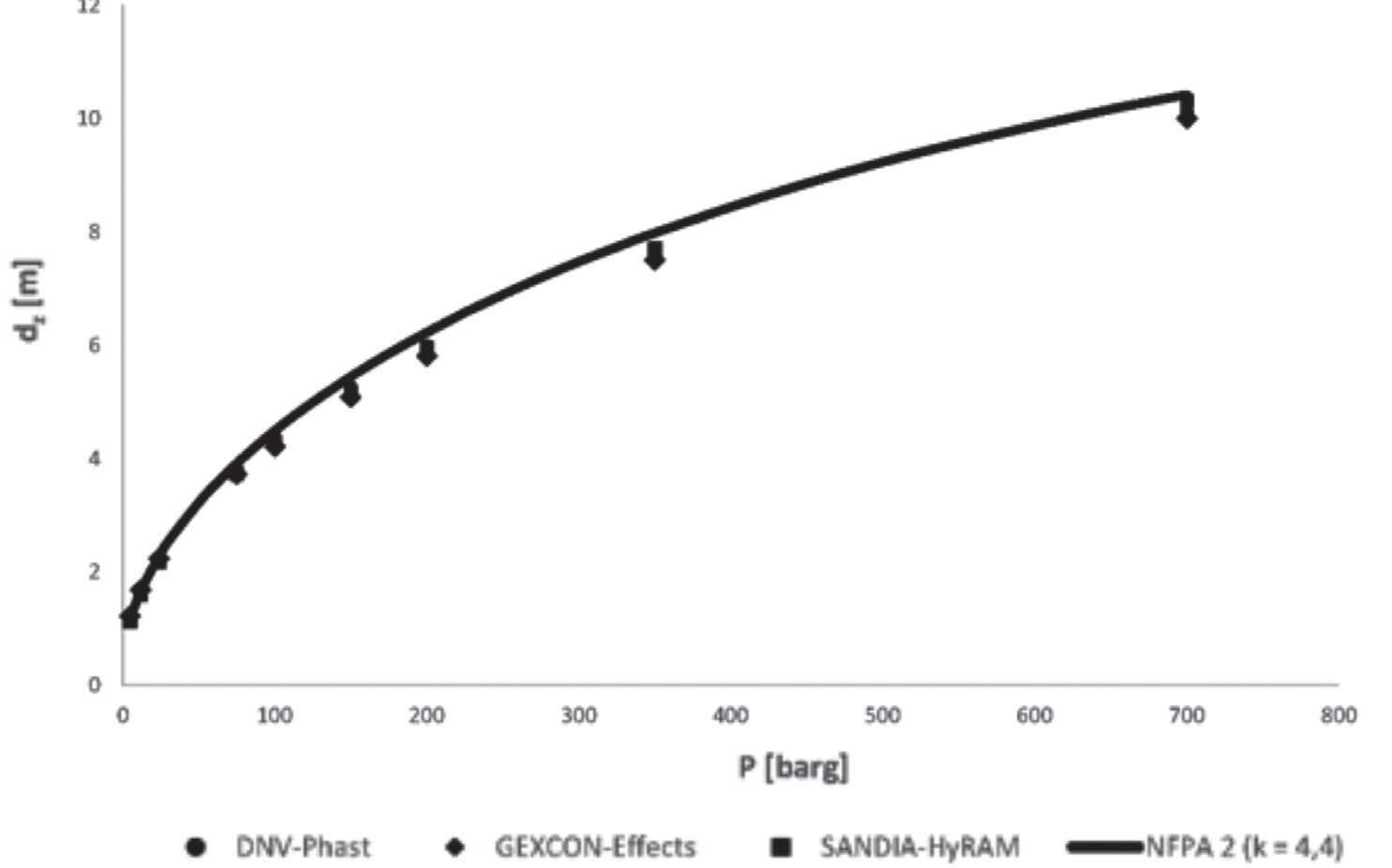
Se invece procediamo ad una verifica con un’altra sostanza spesso coinvolta in problematiche di classificazione ATEX per rilascio a getto, il metano, la sostanziale concordanza dei vari algoritmi di calcolo contenuti nei codici sorgente viene meno. Assumendo il seguente range di simulazione:
-
Metano (M = 16,04 kg/kmol)
-
dj = 1,784 mm (S = 2,5 mm2)
-
P = 5 – 225 bar
-
k = 5,32 (k = 4,4)
Appare evidente una certa disuniformità nei risultati probabilmente attribuibile alla differenza di approccio dei vari modelli implementati. Tali inconsistenze appaiono credibilmente legate anche alle assunzioni fatte da ogni istituto di ricerca sulla variabilità o meno della costante di trasporto e/o sul livello base di riferimento di questo importante parametro.
Figura 12.8 – Benchmark tra software e modello NFPA 2:2023, Metano, d = 1,784 mm, P = 5-225 bar
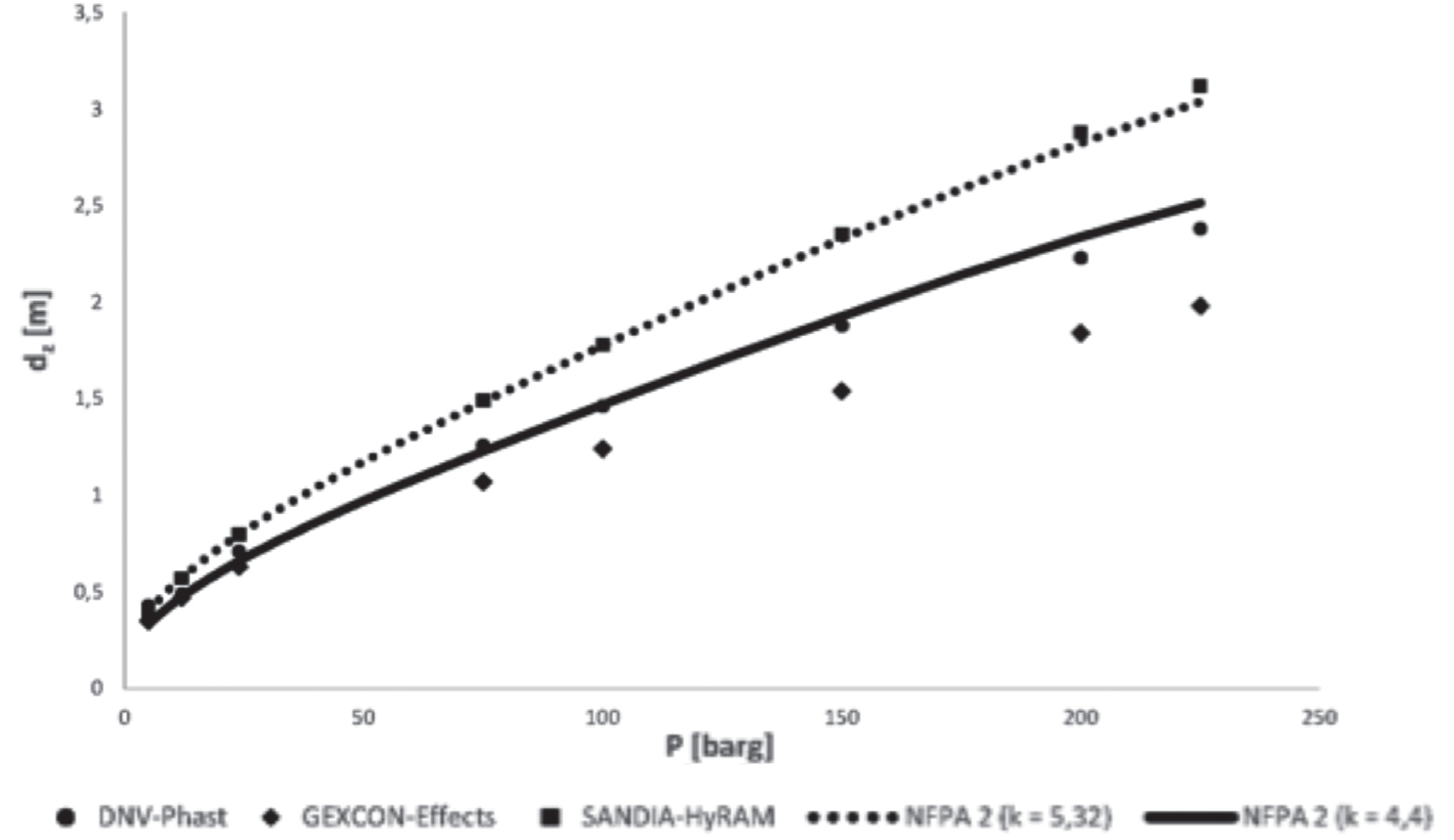
Riepilogando, quindi, l’assunzione di un valore della costante di trasporto tale da far collimare i risultati del modello con quelli delle sperimentazioni dell’idrogeno (k = 4,4) potrebbe determinare una leggera sottostima delle distanze a rischio di esplosione nei casi di gas con masse molari superiori (metano, gas naturale, propano, etilene). Per converso, tarare il “k” a 5,4, come suggerito da Birch basandosi sul gas naturale, produce una decisa sovrastima6 delle zone ATEX per i rilasci e dispersioni di idrogeno grandemente sottoespanso7.
12.6 Alcune ATEX-annotazioni
Stante la conoscenza dei limiti intrinseci della modellistica di campo vicino, per i rilasci a getto è chiara l’importanza di assumere una concentrazione target che consenta il calcolo della distanza zone a rischio di esplosione con un adeguato margine di sicurezza.
In termini più espliciti: “Il dz deve essere correlato all’LFL o all’LFL/2”?
L’assunzione di un k = f.lin(M)8 consente di adeguare progressivamente la distanza di rilascio alla massa molare del gas e alle conoscenze empiriche accumulate nel corso degli ultimi quarant’anni: potrebbe, in questa ipotesi, essere sufficiente un calcolo della distanza fino al solo LFL. Diversamente, voler assumere un k costante tarato sull’idrogeno e al contempo garantire un adeguato margine di sicurezza orienterebbe verso una scelta di una distanza a rischio di esplosione che “legga” l’LFL/2 (almeno per i gas a maggior massa molare dell’idrogeno).
Altresì, stante il vantaggio di sicurezza intrinseco del modello jet presentato nello Yellow Book del TNO olandese, il calcolo sull’LFL porge distanze a rischio di esplosione in ogni caso conservative9.
Quindi, riepilogando, il vantaggio di sicurezza è garantito nei seguenti casi:
-
k = f.lin(M), con kmin = 4,4 (H2). In questo caso la concentrazione di sicurezza è sufficiente sia pari all’LFL;
-
k = 4,4, costante. In questo caso è opportuno orientarsi all’LFL/2 per tutti i gas, idrogeno escluso per il quale l’LFL è concentrazione di sicurezza;
-
TNO-Yellow Book. L’LFL restituisce valori di dz sempre in vantaggio di sicurezza.
È necessario prestare molta attenzione, tuttavia, nel considerare come esclusiva misura della zona a rischio di esplosione l’estensione dz fino all’LFL (o all’LFL/2) di un getto libero. La presenza di ostacoli alla libera dispersione (es. pipe-rack) può, infatti, raddoppiare la distanza a rischio di esplosione (Colombini et al., 2021). Inoltre, la dispersione in prossimità del suolo può causare, per “effetto Coanda”10, estensioni dell’ATEX fino a quattro volte maggiori rispetto al calcolo con getto libero (Colombini et al., 2020).
In ogni caso tutte le emissioni degli energy carrier sono, per definizione, estese poiché superano, negli stoccaggi, le pressioni indicate nell’art. 4.4.2, CEI EN IEC 60079-10-1:2021.
12.7 Esempi di calcolo
12.7.1 Classificazione dovuta ad un rilascio di idrogeno supercritico
Prima di affrontare il tema connesso alla classificazione legata alla presenza di idrogeno supercritico, riepiloghiamo le principali caratteristiche ATEX di questa sostanza.
-
Il campo d’infiammabilità in aria è molto ampio [4÷77%] e la variazione della MIE, nel range di tali concentrazioni, risulta particolarmente accentuata, raggiungendo il minimo a circa il 28% [LMIE11 = 0,016 mJ].
-
In presenza di solo ossigeno, a pressione atmosferica, l’ampiezza del campo di infiammabilità dell’idrogeno si estende in modo rilevante [4÷95%] e la MIE si riduce di un ordine di grandezza [LMIE = 0,0012 mJ]. La miscela diviene pertanto estremamente pericolosa, specialmente se confinata, poiché “sempre” infiammabile ed innescabile in presenza di energie statiche davvero minime.
-
In condizioni atmosferiche il gas è incolore e inodore. Non è tossico ma può causare asfissia.
-
L’idrogeno possiede un coefficiente Joule-Thomson negativo a temperature superiori a –73 °C:

-
L’espansione isoentalpica determina il riscaldamento del gas che aumenta, a sua volta, la sua tendenza al galleggiamento. Per esempio, un’espansione laminare da 1000 bar fino alla pressione ambiente causa un incremento di circa 50 °C nel fluido rilasciato. Questo aumento di temperatura non è tuttavia sufficiente ad accendere l’idrogeno [Tacc = 560 °C].
-
La temperatura di fiamma alla concentrazione del 19,6% in volume è pari a 2318 K.
-
I parametri di esplodibilità: Pmax = 6,8 bar, Kg = 550 bar m/s.
-
A tenuta d’aria non significa a prova d’idrogeno: con la prevista introduzione su larga scala dell’idrogeno come vettore energetico, la sua perdita volumetrica dai contenitori e dalle condutture potrebbe risultare fino a tre volte maggiore della perdita di metano gassoso.
-
L’idrogeno gassoso puro è circa 14 volte più leggero dell’aria in condizioni normali e questo è il motivo per cui qualsiasi perdita si sposta rapidamente verso l’alto. Tuttavia, a mano a mano che un rilascio a getto si impoverisce la dispersione diviene meno “jet” e la tendenza al galleggiamento si attenua di molto.
-
Il coefficiente di diffusione dell’idrogeno (0,61 cm2/s) è circa quattro volte superiore a quello del metano (0,16 cm2/s)
-
La velocità di galleggiamento dell’H2 puro è compresa tra 1,2 e 9,1 m/s (circa il doppio di quella del metano)
-
Una fiamma idrogeno-aria è quasi invisibile alla luce del giorno e irradia principalmente nella regione dell’infrarosso e dell’ultravioletto. Qualsiasi visibilità della zona di combustione dell’idrogeno è dunque causata da impurità o da particelle incandescenti presenti nell’aria e investite dalla fiamma.
La Norma ISO 19880-1:2020 evidenzia una certa variabilità normativa in tema di scelta della sezione di guasto.
Le linee guida EIGA IGC Doc 121/14 (Hydrogen pipelines system) indicano, al §4.6.4 (Scenari di eventi tipici), le seguenti specifiche: “[…] Per facilità di analisi, gli eventi frequentemente considerati sono:
-
la rottura a ghigliottina;
-
il 50% della sezione completa;
-
una piccola perdita (5% del foro completo).
È solo quest’ultimo che ricade nel campo di applicazione della Norma CEI EN IEC 60079-10-1:2021 poiché i primi due scenari sono tipici eventi catastrofici da valutare nell’ambito della direttiva Seveso III.
Sempre a questo proposito la Norma NFPA 20:2023 (Hydrogen Technologies Code) nell’allegato E (Determination of Separation Distances for Bulk Gaseous Hydrogen Systems) specifica preliminarmente che le distanze pericolose indicate nelle Norme NFPA 55 e NFPA 2 si basano sulla previsione delle caratteristiche di:
-
rilasci non innescati;
-
Jetfire;
derivanti da perdite di idrogeno.
Poiché le caratteristiche degli scenari appena riassunti dipendono dalla pressione interna del gas e dalla superficie effettiva della perdita, l’NFPA 20 fornisce una Tabella suddivisa in quattro range di pressione a cui corrispondono specifici diametri di tubazione.
In particolare, il calcolo del diametro effettivo della perdita per ciascun intervallo di pressione è basato sul diametro caratteristico della tubazione (I.D. = diametro interno): l’area della sorgente di emissione risulterà quindi pari al 3% dell’area del flusso nel tubo.
Per una perdita con sezione circolare il diametro effettivo della sorgente di emissione sarà dunque uguale a:

La seguente Tabella 12.2 correla l’intervallo di pressione relativa interna al diametro interno (I.D.) della tubazione convogliante idrogeno.
Tabella 12.2 – Relazione tra pressione e diametro interno delle tubazioni convoglianti H2
| Pressione relativa, p [kPag] | Diametro caratteristico interno (I.D.) Dpipe,ID |
|---|---|
| 103 < p ≤ 1724 | 52,5 |
| 1724 < p ≤ 20684 | 18,97 |
| 20684 < p ≤ 51711 | 7,92 |
| 51711 < p ≤ 103421 | 7,16 |
Fonte: NFPA 2:2023
Tabella 12.3 – Parametri di infiammabilità dell’idrogeno
| Sostanza infiammabile | Idrogeno (cas n. 1333-74-0) |
| Massa molare [Mgas] | 2,016 kg/kmol |
| Pressione critica | 13,13 bar |
| Temperatura critica | -239,96 °C |
| Flashpoint [FP] | -259,15 °C |
| Limite inferiore di infiammabilità [LFL] | 4% |
| Temperatura di autoaccensione [AIT] | 560 °C |
| Sorgente di emissione [SE] | Tubazione NFPA 2:2023 |
| Grado di emissione | Secondo |
| Coefficiente d’efflusso [Cd] | 0,62 (bordi a spigolo) |
| Superficie di emissione [S] | Cfr. argomentazioni successive |
| Pressione nel contenimento [P0] | 700 bar |
| Costante specifica dei gas [R] | 8314 J/kmol K |
| Fattore di comprimibilità [Z0] | Cfr. argomentazioni successive |
| Rapporto tra i calori specifici [γ] | Cfr. argomentazioni successive |
| Gruppo e classe di temperatura | IICT1 |
Fatta questa premessa si vuole procedere a determinare le zone a rischio di esplosione di un sito di rifornimento di auto alimentate ad idrogeno nella zona delle tubazioni pressurizzate a 700 bar.
Le caratteristiche principali dell’infiammabile, riportate nella seguente Tabella 12.4, sono estratte dalla Norma EN ISO IEC 80079-20-1:2019 integrata con parametri estratti da DIPPR 801
Le caratteristiche di ventilazione sono le seguenti:
Tabella 12.4 – Caratteristiche dell’ambiente di rilascio
| Ambiente | Esterno. Luogo relativamente privo di ostacoli (f = 2) |
| Presidio | Luogo sottoposto a generica sorveglianza nel quale, in occasione di anomalie, è credibile un intervento di bonifica in un tempo non superiore a 90 min |
| Pressione ambiente [pa] | 1,01325 bar |
| Temperatura ambiente [Ta] | 20 °C |
| Altezza di rilascio [hr] | ≌ 2,5 m |
| Velocità dell’aria [UW] | Cfr. argomentazioni successive |
| Disponibilità della ventilazione | Cfr. argomentazioni successive |
Il coefficiente di espansione politropica viene calcolato in base al cp del gas ideale, riprodotto nella seguente Figura 12.9.
Figura 12.9 - cp al variare dalla temperatura, hp gas ideale
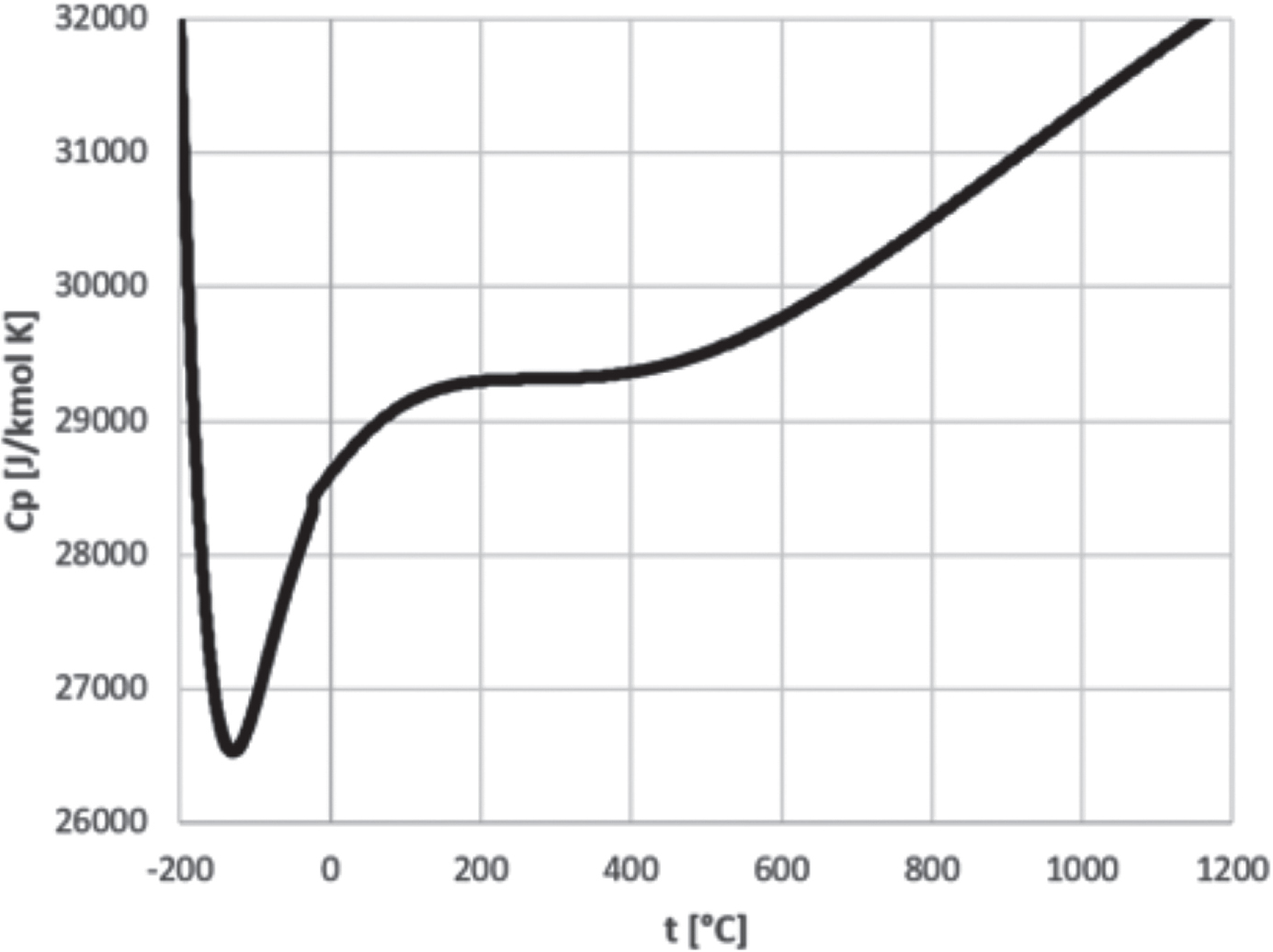
Fonte: DIPPR 801
Si ricava, alla temperatura di 20 °C, il seguente parametro:
-
cp = 28,74 kJ/kmol K
Il coefficiente di espansione politropica sarà quindi calcolato con la seguente espressione:

Il gas in uscita dalla sorgente di emissione è di tipo leggero, come si desume dal seguente calcolo:
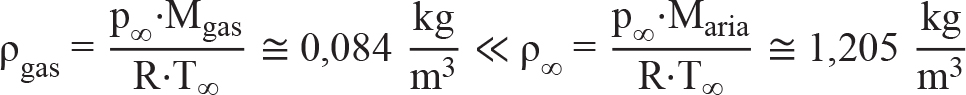
Tenendo in considerazione questo aspetto unito all’altezza di rilascio (hr ≌ 2,5 m) nonché all’area relativamente priva di ostacoli (f = 2) si ottiene, dalla Tabella C.1, CEI EN IEC 60079-10-1:2021, la velocità di ventilazione dell’aria:

L’ampiezza del foro di guasto della sorgente di emissione in tubazioni idrogeno pressurizzate a 700 bar si ottiene applicando la Norma NFPA 2:2023. Si ha:
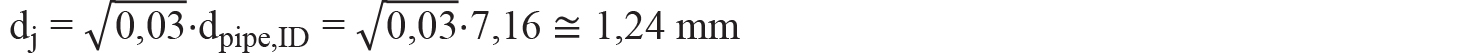
A cui corrisponde una sezione di foro di guasto non inferiore a:

Il valore di sezione di guasto calcolato appare compatibile con le previsioni stabilite in Tabella B.1, EN IEC 60079-10-1:2021.
La portata della sorgente di emissione è calcolata con l’equazione B.5, EN IEC 60079-10-1:2021. Si ha:
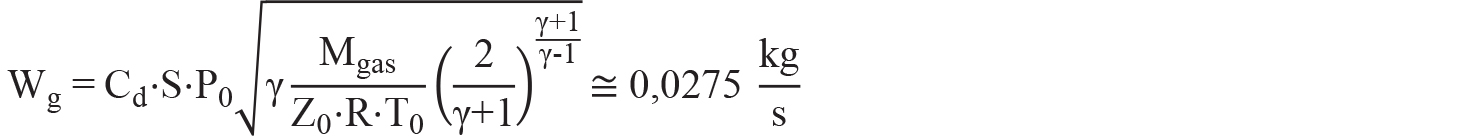
dove:
Z0 = 1,422 [Fonte: DIPPR 801. SVR(20 °C) = 0,014682 m3/kmol]
Si ottengono i seguenti parametri di derivazione.

Il grado di diluizione è quindi di tipo MEDIO. In ogni caso, essendo la pressione molto superiore al limite massimo di 10 bar specificato nell’art. 4.4.2, CEI EN IEC 60079-10-1:2021, la diluizione non potrà considerarsi ALTA.
Figura 12.10 – Determinazione del grado di diluizione
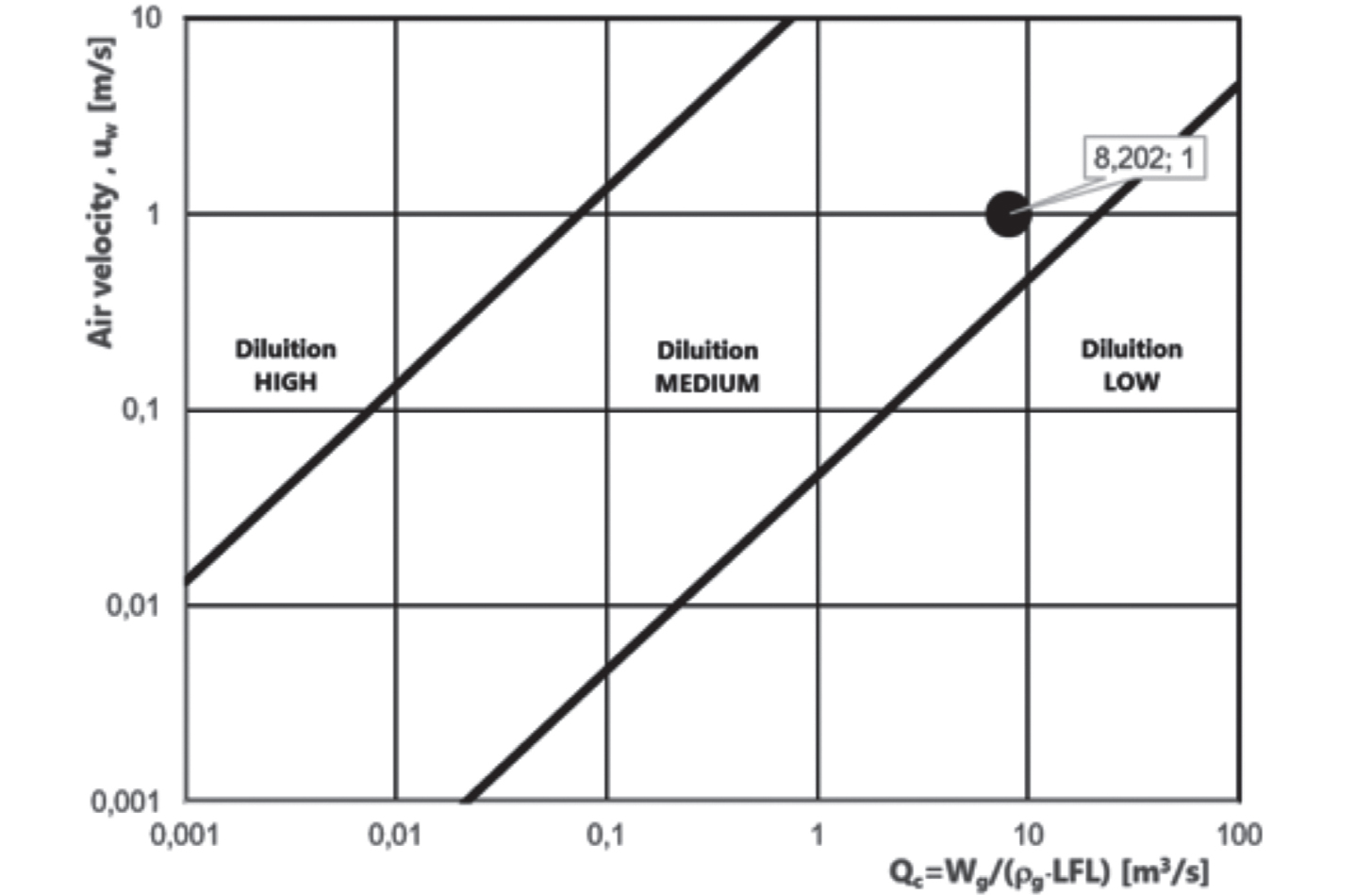
Fonte: Allegato C, CEI EN IEC 60079-10-1:2021
La densità del gas all’interno del contenimento in pressione è la seguente:

Facendo riferimento allo schema di Figura 12.3 si procede al calcolo della pressione nel bordo d’uscita:

La temperatura presente nel bordo d’uscita è invece la seguente:

Attraverso questi due parametri è possibile il calcolo della compressibilità del gas all’uscita “j”:
Zj = 1,234 [Fonte: DIPPR 801. SVR(-29,3 °C) = 0,012832 m3/kmol]
La densità del gas al bordo fisico d’uscita è quindi la seguente:

Si noti come, a fronte di un (circa) dimezzamento della pressione sul bordo d’uscita, la densità si riduce molto meno a causa sia della variazione della compressibilità sia della marcata riduzione della temperatura.
La velocità del suono del gas in condizioni di completa sottoespansione è invece la seguente:

Mentre la velocità al termine della fase di espansione in atmosfera è rappresentata dall’equazione riportata appresso.

Lo pseudo-diametro verrà quindi calcolato con la seguente equazione:

Si noti come sia circa dieci volte superiore al diametro reale. Con questo parametro è ora possibile determinare la distanza a rischio di esplosione. Si ha:
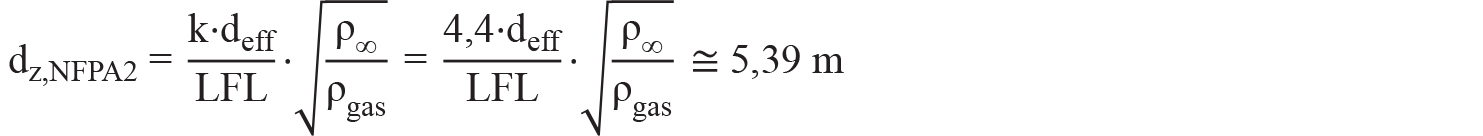
Che, arrotondato per eccesso al multiplo di 0,5 m più prossimo, restituisce:
dz,NFPA2 = 5,5 m
Per confronto, la distanza di classificazione calcolata con la metodologia prevista dal TNO-Yellow Book indica il seguente valore (cfr. ebook ATEX già citato nella nota 8):
dz,YB ≅ 8,5 m
Il calcolo eseguito con DNV-Phast (Vessel Leak) restituisce il medesimo risultato di NFPA 2:2023:
dz,Phast ≅ 5,5 m
Figura 12.11 – Determinazione dell’estensione svolta con DNV-Phast (Vessel Leak), vista in prospetto
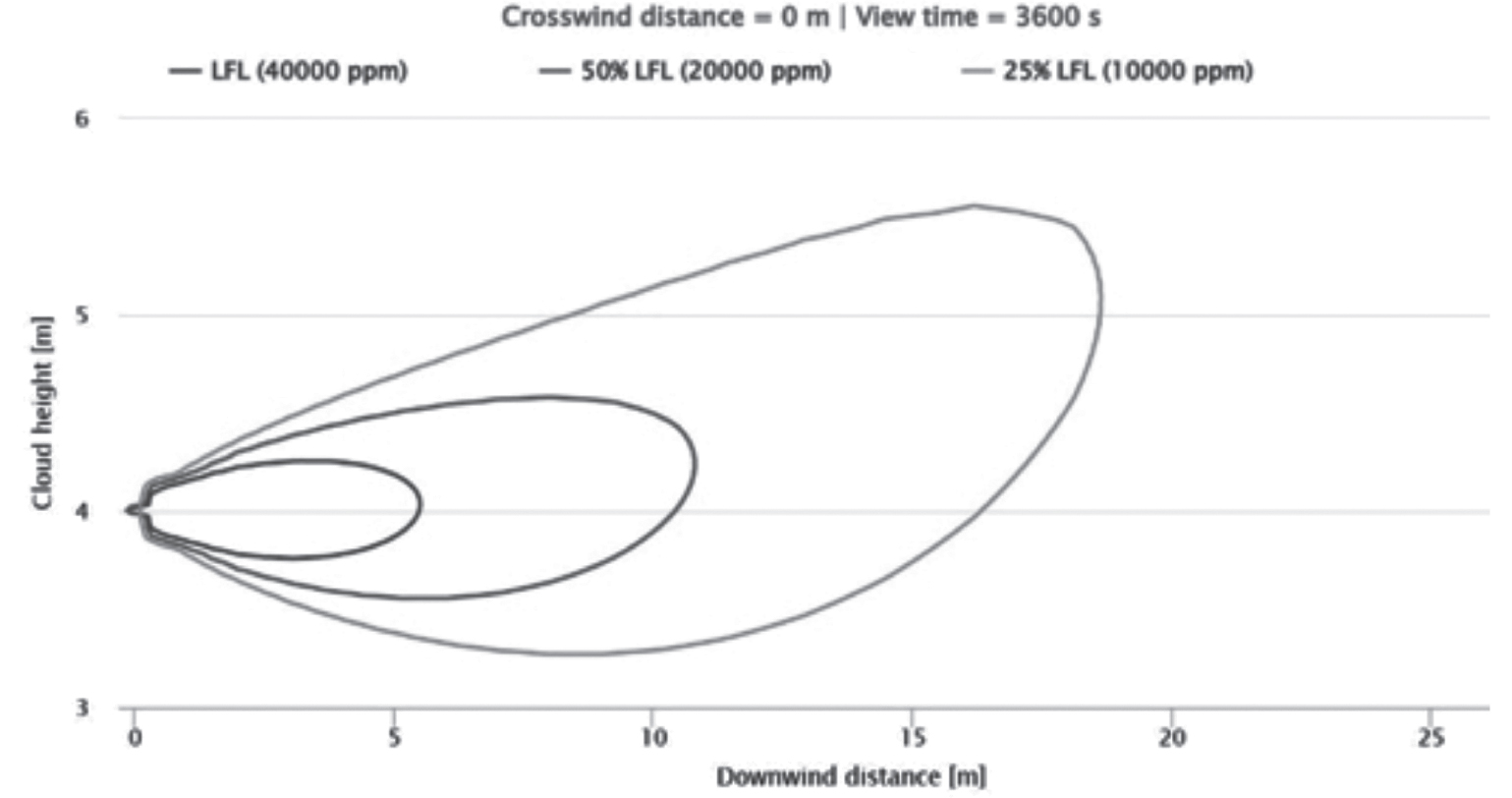
Anche la simulazione implementata con GEXCON-Effects quantifica la distanza di classificazione dell’ordine di quanto calcolato con il modello NFPA 2:2023:
dz,Effects ≅ 5,46 m
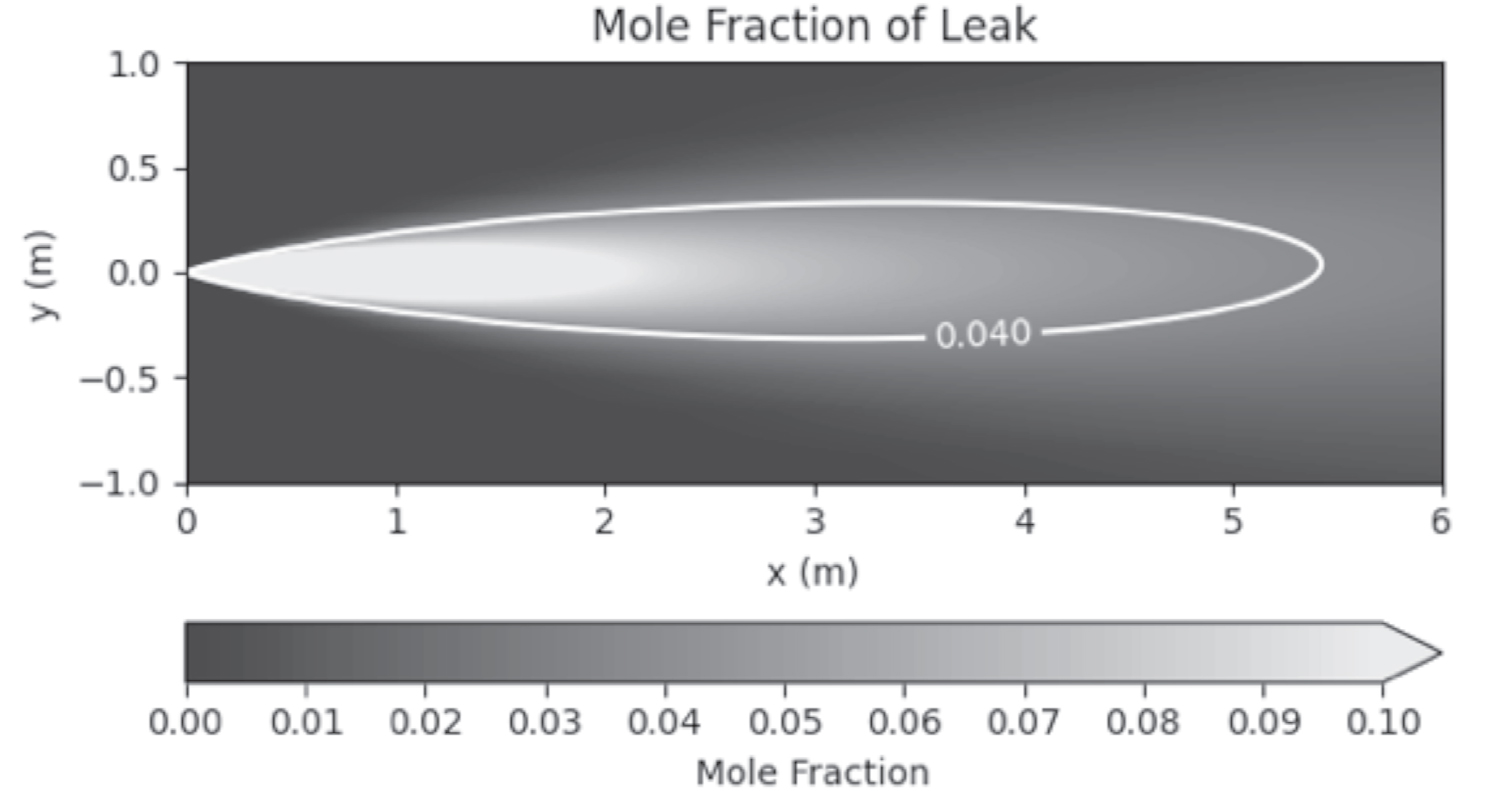
Figura 12.12 – Determinazione dell’estensione svolta con GEXCON-Effects V12, vista in pianta
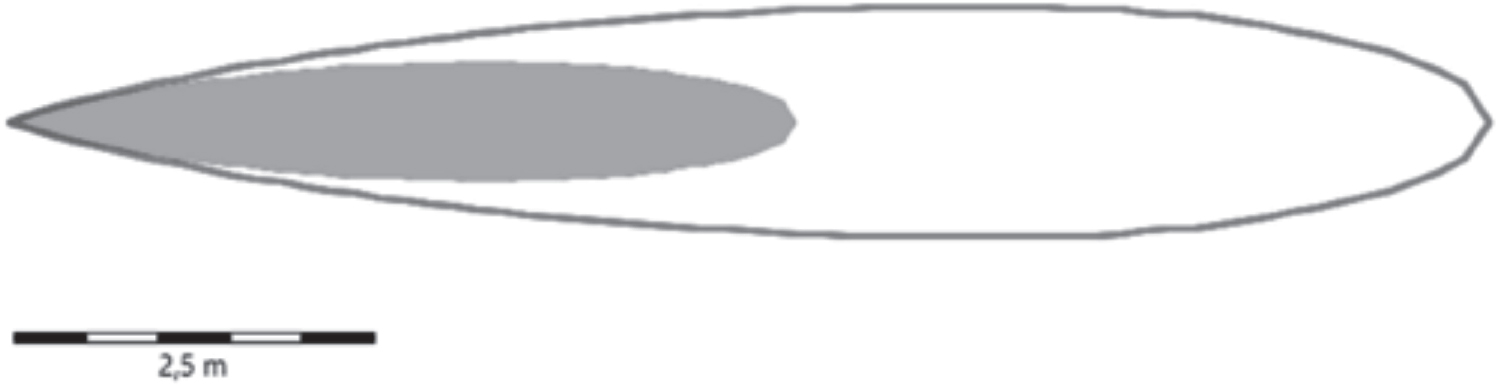
Infine, la simulazione implementata con HyRAM+ v5.0 di SANDIA: la distanza di classificazione risulta anch’essa sovrapponibile a quanto calcolato con il modello NFPA 2:2023:
dz,HyRAM+ ≅ 5,55 m
Figura 12.13 – Determinazione dell’estensione svolta con HyRAM+ v5.0 di SANDIA, vista in prospetto (Modello di Yoceil/Otugen)
Con i seguenti descrittori inseriti nella successiva matrice di classificazione:
-
Grado della sorgente di emissione: SECONDO
-
Disponibilità della ventilazione: ADEGUATA12
-
Grado della diluzione: MEDIO
si ottiene una zona di tipo 2 IICT1 estesa.
Tabella 12.5 – Matrice di classificazione (cfr. allegato D, EN IEC 60079-10-1:2021)13| Grado di emissione | Efficacia della ventilazione | ||||||
|---|---|---|---|---|---|---|---|
| Diluizione Alta | Diluizione Media | Diluizione Bassa | |||||
| Disponibilità della ventilazione | |||||||
| Buona | Adeguata | Scarsa | Buona | Adeguata | Scarsa | Buona, adeguata o scarsa | |
| Continuo | Non hazardous [Zona 0NE]1 | Zona 2 [Zona 0NE]1 | Zona 1 [Zona 0NE]1 | Zona 0 | Zona 0 + Zona 23 | Zona 0 + Zona 1 | Zona 0 |
| Primo | Non hazardous [Zona 1NE]1 | Zona 2 [Zona 1NE]1 | Zona 2 [Zona 1NE] | Zona 1 | Zona 1 + Zona 2 | Zona 1 + Zona 2 | Zona 1 oppure Zona 04 |
| Secondo2 | Non hazardous [Zona 2NE]1 | Non hazardous [Zona 2NE]1 | Zona 2 | Zona 2 | Zona 2 IICT1 | Zona 2 | Zona 1 e persino Zona 04 |
A titolo di confronto si utilizza l’equazione f.GB.5.1-5a, ex CEI 31-35:2012 che fornisce valori affidabili e riproducibili in presenza di equilibrio termico tra lo stoccaggio del gas pressurizzato e la temperatura ambiente. Si ha:

Risultato paragonabile a quello ottenuto con l’equazione TNO-Yellow Book ma molto più ampio della distanza calcolata con la metodologia NFPA 2:2023.
La determinazione della distanza pericolosa svolta invece in base diagramma logaritmico dell’allegato D, CEI EN IEC 60079-10-1:2021 è di seguito riportata. Purtroppo, l’assenza di informazioni sulla costruzione del diagramma logaritmico non consente di fare inferenze approfondite sul significato del fenomeno fisico che viene parametrizzato.
Figura 12.14 – Determinazione della distanza pericolosa

Fonte: Allegato D, CEI EN IEC 60079-10-1:2021
La dz,NFPA2 sembra essere il modello maggiormente aderente agli attuali standard tecnici di riferimento (il software HyRAM+ v5.0 di SANDIA, con il quale il valore calcolato è in accordo, è citato, quale “gold standard”, in UNI ISO 19880-1:2020): assumiamo definitivamente che la distanza a rischio di esplosione sia quella calcolata con il modello NFPA 2:2023. Si ha:
r = dz = dz,NFPA2 = 5,5 m
Poiché la direzione di rilascio non è nota, la forma sarà quella di una sfera centrata sulla sorgente di emissione.
La forma della zona classificata possiede, in conclusione, le seguenti caratteristiche:
-
Estensione, dz = r = 5,5 m a partire dalla sorgente di emissione, con estensione verso il basso non superiore alla distanza hr.
-
Forma: sferica (Fonte: IEC, 2021)
Figura 12.15 – Forma della zona classificata
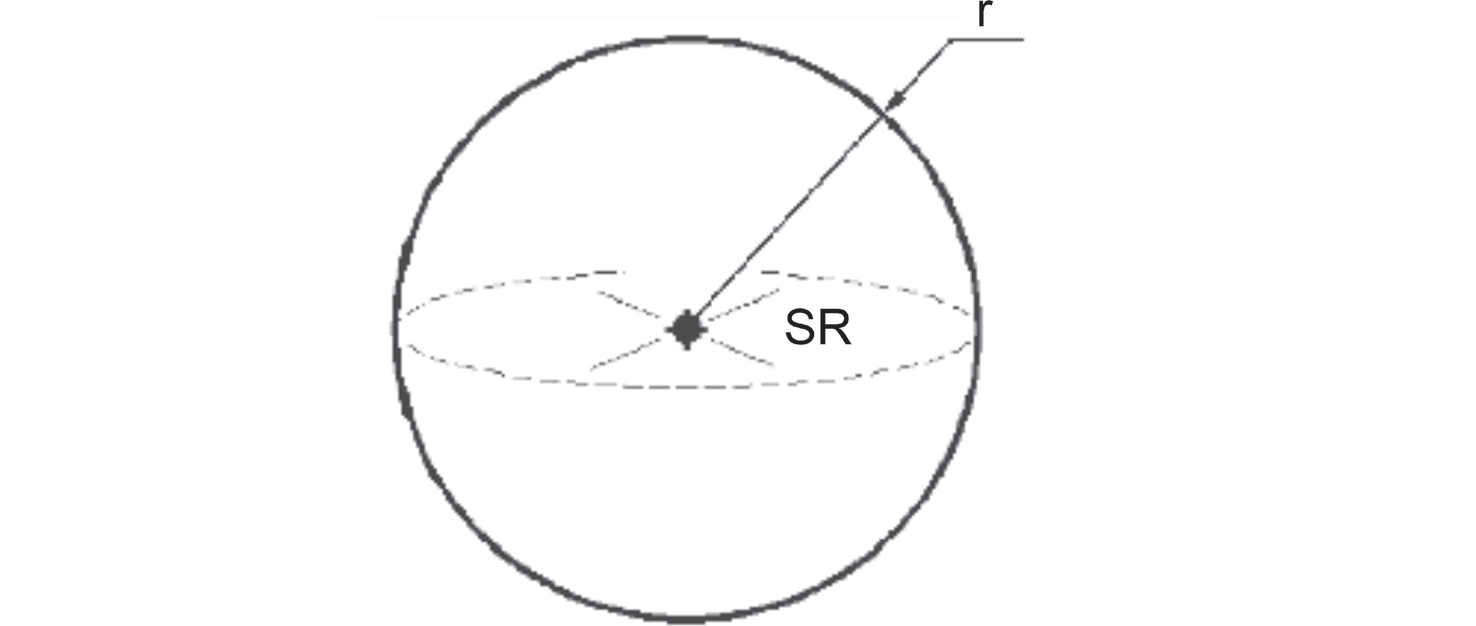
Fonte: IEC, 2021
12.7.2 Classificazione della zona a rischio di esplosione dovuta alla presenza di una PSV di boil off in un serbatoio criogenico contenente LNG destinato al trasporto stradale
Premessa tecnica: il gas naturale liquefatto (LNG) rispetto a quello compresso (CNG) possiede l’innegabile vantaggio energetico di riuscire a stoccare in un litro di liquido l’equivalente di 600 litri gassosi in condizioni atmosferiche. Poiché, tuttavia, la temperatura ambiente è di molto superiore a quella critica, l’attraversamento della curva Liquido-Vapore (LV) può avvenire solo per raffreddamento criogenico poiché la strada della compressione, tipica dell’LPG, non risulta praticabile.
Il campo di variabilità delle temperature, all’interno del contenitore criogenico, oscilla da un minimo di circa −161 °C in corrispondenza della pressione atmosferica ad un massimo pari a −112 °C alla pressione di attivazione della PSV primaria di boil off (cfr. seguente Figura 12.16). In generale alle condizioni operative standard un serbatoio criogenico di stoccaggio di LNG possiede tempi di ritenzione dichiarati dal costruttore superiori a 5 giorni. In tale intervallo di tempo il serbatoio scaricherà parte del suo contenuto in atmosfera a causa del progressivo riscaldamento.
Figura 12.16 – Diagramma di stato del metano integrato con le pressioni di riferimento di un tipico serbatoio criogenico per uso in veicoli stradali
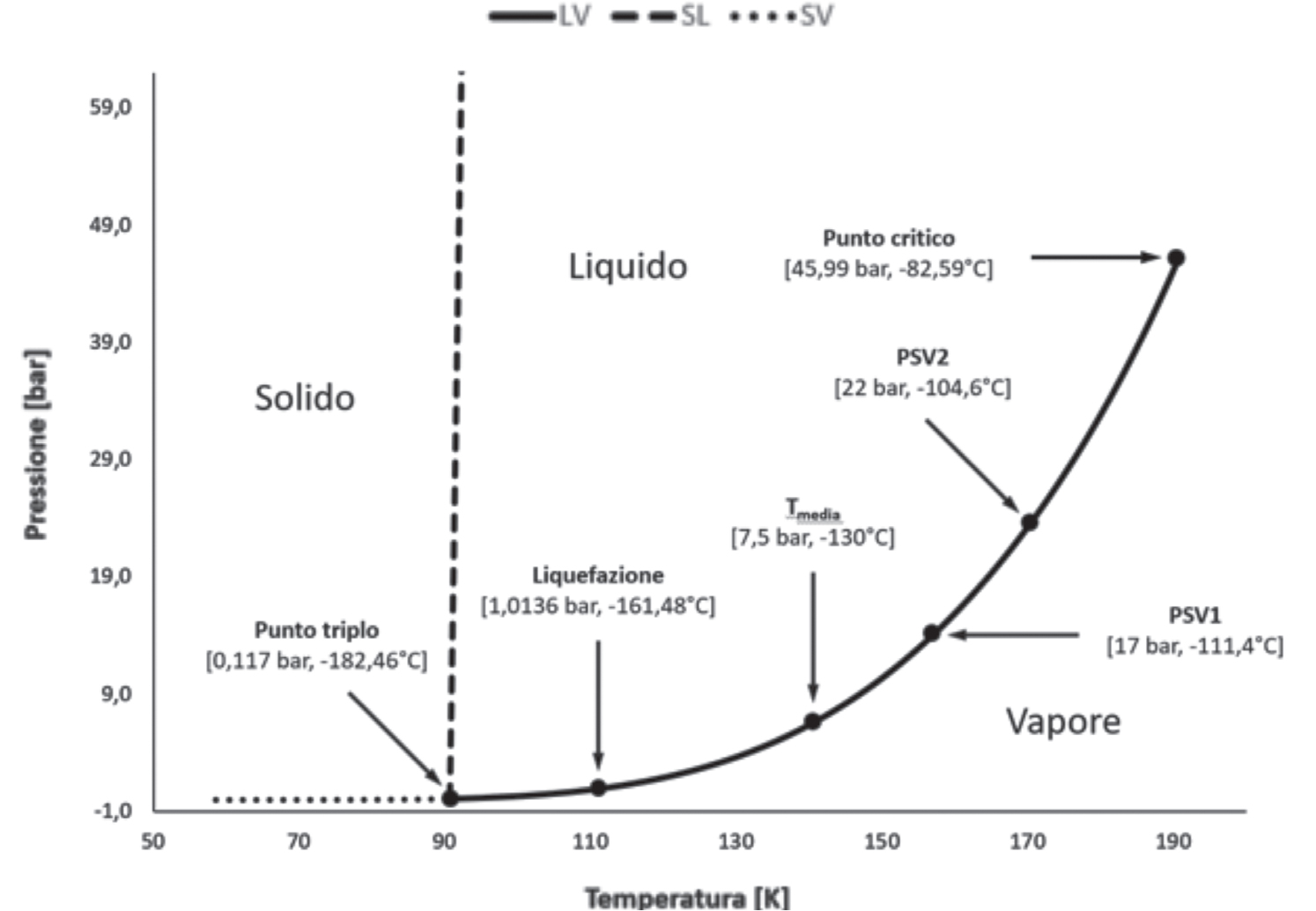
(Fonte: Air Liquide)
Studio del caso: un serbatoio criogenico di LNG, destinato all’alimentazione del motore di un trattore stradale, è dotato delle seguenti due valvole di sicurezza:
-
PSV1: chiamata valvola di sicurezza primaria, è tarata a 17 bar e protegge il serbatoio criogenico dalle normali fasi di riscaldamento dell’LNG presente all’interno (“Boil off”). L’uscita è convogliata con tubazioni che sfociano nella parte più alta del mezzo;
-
PSV2: chiamata valvola di sicurezza secondaria, è tarata a 22 bar e interviene nel caso in cui la valvola primaria si guasti o intervengano fattori e malfunzionamenti rari. L’apertura della valvola, destinata a proteggere un recipiente PED qualificato a 30 bar, è da ritenersi guasto catastrofico e pertanto escluso dall’ambito della classificazione delle zone a rischio di esplosione14. Tale valvola possiede un tappo rosso di materiale plastico: la sua mancanza in sede indica l’azionamento della PSV2 e sarà necessario agganciare, a tale avvenimento, delle specifiche procedure di gestione.
La PSV1 primaria installata a protezione del serbatoio possiede le seguenti caratteristiche:
-
S = 40 mm2 (sezione dell’orifizio di scarico)
-
p = 17 bar (pressione di attivazione)
La sorgente di rilascio connessa alla PSV1 avrà quindi i seguenti gradi di emissione:
-
Primo grado con sezione di guasto pari a S = 4 mm2. La pressione di emissione sarà quella relativa alla tensione di vapore corrispondente alla temperatura media presente nel contenimento.
-
Secondo grado15 con sezione di guasto pari a S = 40 mm2 e p = 17 bar.
Per semplicità di trattazione ci occuperemo del solo secondo grado (il calcolo del primo grado è perfettamente sovrapponibile a quanto già visto con l’esercizio relativo alla PSV del serbatoio di propano svolto nel Capitolo 4. Nel caso del propano, tuttavia, si erano escluse emissioni di secondo grado).
Le caratteristiche principali dell’infiammabile, riportate nella seguente Tabella 12.6, sono estratte dalla Norma EN ISO IEC 80079-20-1:2019 integrata con parametri estratti da DIPPR 801.
Tabella 12.6 – Parametri di infiammabilità del metano
| Sostanza infiammabile | Metano (cas n. 74-82-8) |
| Massa molare [Mgas] | 16,04 kg/kmol |
| Pressione critica | 45,99 bar |
| Temperatura critica | -82,586 °C |
| Flashpoint [FP] | -186,03 °C |
| Limite inferiore di infiammabilità [LFL] | 4,4% |
| Temperatura di autoaccensione [AIT] | 600 °C |
| Sorgente di emissione [SE] | Scarico di boil off da PSV1 |
| Grado di emissione | Secondo16 |
| Coefficiente d’efflusso [Cd] | 0,85 (bordi arrotondati) |
| Superficie di emissione [S] | 40 mm2 |
| Pressione nel contenimento [P0] | 17 bar |
| Costante specifica dei gas [R] | 8314 J/kmol K |
| Fattore di comprimibilità [Z0] | Cfr. argomentazioni successive |
| Rapporto tra i calori specifici [γ] | Cfr. argomentazioni successive |
| Gruppo e classe di temperatura | IIAT1 |
Le caratteristiche di ventilazione sono le seguenti riportate in Tabella 12.7:
Tabella 12.7 – Caratteristiche dell’ambiente di rilascio
| Ambiente | Esterno Luogo privo di ostacoli (f = 1) |
| Presidio | Luogo non presidiato |
| Pressione ambiente [pa] | 1 bar |
| Temperatura ambiente [Ta] | 20 °C |
| Altezza di rilascio [hr] | ≤ 2 m |
| Velocità dell’aria [UW] | 0,5 m/s (cfr. Table C.1, EN IEC 60079-10-1:2021) |
| Disponibilità della ventilazione | Buona17 (ventilazione esterna sempre presente) |
Il coefficiente di espansione politropica viene calcolato in base al cp del gas ideale, riprodotto nella seguente Figura 12.17.
Figura 12.17 – cp al variare dalla temperatura, hp gas ideale
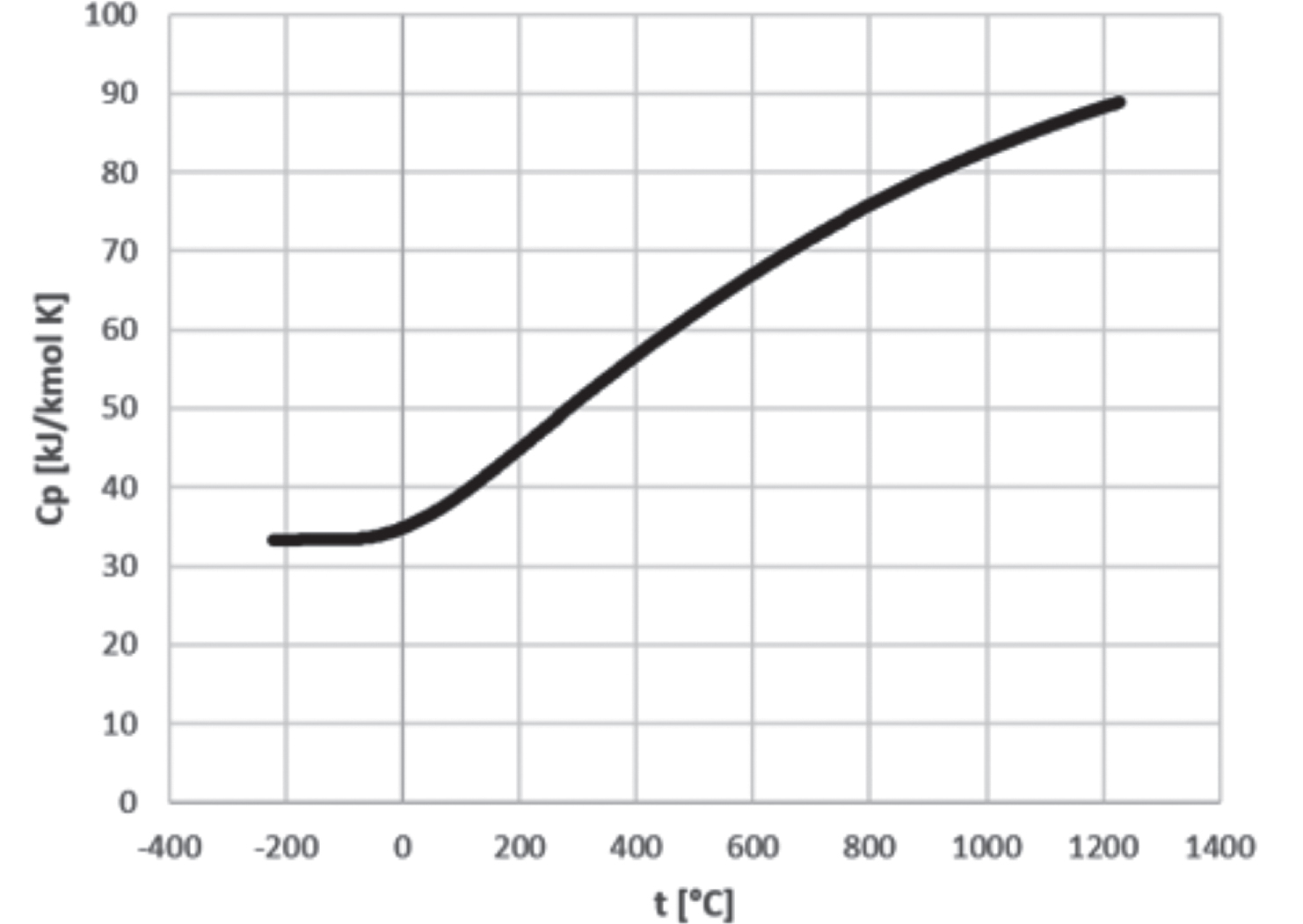
Fonte: DIPPR 801
Si ricava, alla temperatura di -111,4 °C, il seguente parametro:
-
cp = 33,327 kJ/kmol K
Il coefficiente di espansione politropica sarà quindi calcolato con la seguente espressione:

La procedura di calcolo che verrà seguita farà riferimento allo schema di rilascio di gas sottoespanso già indicato negli esercizi precedenti.
Il gas in uscita dalla sorgente di emissione, nell’ipotesi assuma rapidamente la temperatura ambientale, è di tipo leggero, come si desume dal seguente calcolo:
Il gas in uscita dalla sorgente di emissione è di tipo leggero, come si desume dal se-

guente calcolo:
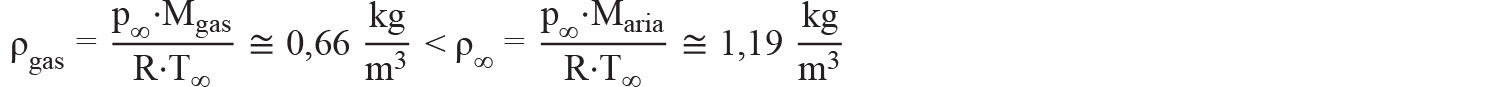
Tenendo in considerazione questo aspetto unito all’altezza di rilascio (hr ≤ 2,5 m) nonché all’area relativamente priva di ostacoli (f = 1) si ottiene, dalla Tabella C.1, CEI EN IEC 60079-10-1:2021, la velocità di ventilazione dell’aria:
L’ampiezza del foro di guasto della sorgente di emissione PSV1 è pari, come indicato, a S = 40 mm2 a cui corrisponde un diametro della sezione dell’orifizio pari a:

La portata della sorgente di emissione è calcolata con l’equazione B.5, EN IEC 60079-10-1:2021. Si ha:
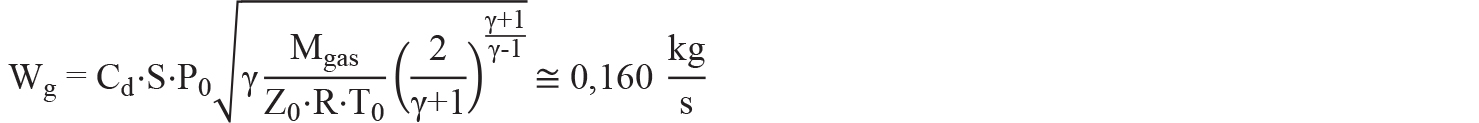
dove:
| Z0 | = 0,74 [Fonte: iterazione di Newton–Raphson su EOS Peng Robinson. Sono possibili altre forme di soluzione (es. NIST WebBook, DIPPR 801, Secondo coefficiente del viriale, ecc.)] |
Si ottengono i seguenti parametri di derivazione.

Il grado di diluizione è quindi di tipo MEDIO. In ogni caso, essendo la pressione superiore al limite massimo di 10 bar specificato nell’art. 4.4.2, CEI EN IEC 60079-10-1:2021, la diluizione non potrà considerarsi ALTA.
Figura 12.18 – Determinazione del grado di diluizione
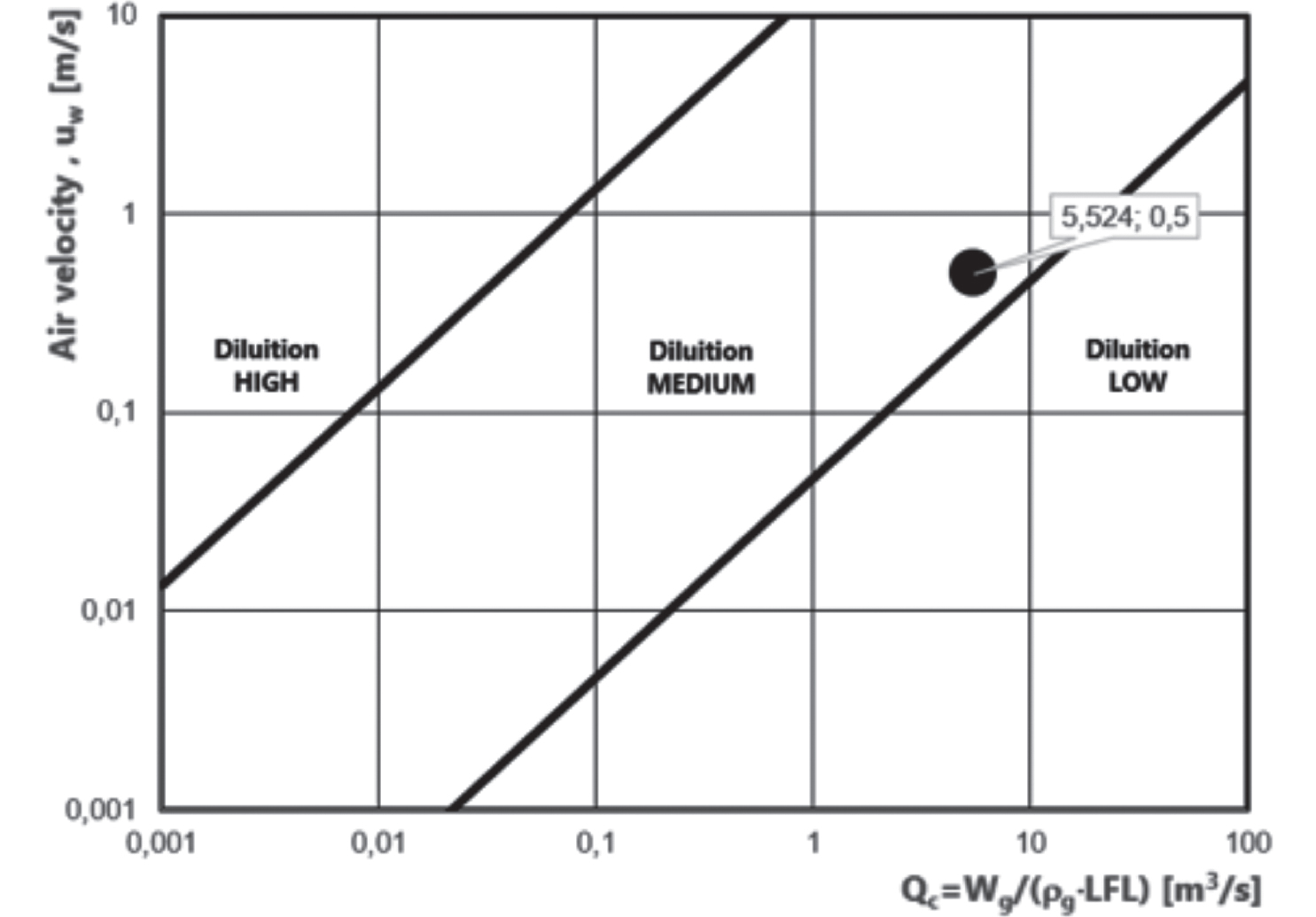
Fonte: Allegato C, CEI EN IEC 60079-10-1:2021
La densità del gas all’interno del contenimento in pressione è la seguente:

Facendo riferimento allo schema di Figura 12.3 si procede al calcolo della pressione nel bordo d’uscita:

La temperatura presente nel bordo d’uscita è invece la seguente:

Attraverso questi due parametri è possibile il calcolo della compressibilità del gas all’uscita “j”:
| Zj | = 0,78 [Fonte: iterazione di Newton–Raphson su EOS Peng Robinson. Sono possibili altre forme di soluzione (es. NIST WebBook, DIPPR 801, Secondo coefficiente del viriale, ecc.)] |
La densità del gas al bordo fisico d’uscita è quindi la seguente:

Si noti che l’elevatissimo sottoraffreddamento del fluido fa sì che la densità dei vapori di metano all’uscita siano circa 14 volte più pesanti dell’aria. Rapidamente, però, tale differenza verrà livellata a causa del riscaldamento del getto e dell’impoverimento della miscela.
La velocità del suono del gas in condizioni di completa sottoespansione è invece la seguente:

Mentre la velocità al termine della fase di espansione in atmosfera è rappresentata dall’equazione riportata appresso.

Lo pseudo-diametro verrà quindi calcolato con la seguente equazione:

Si noti come sia circa quattro volte superiore al diametro reale. Con questo parametro è ora possibile determinare la distanza a rischio di esplosione. Si ha:

dove k è uguale a:
k = 0,065·M + 4,268 ≅ 5,3218
Con i seguenti descrittori inseriti nella successiva matrice di classificazione:
-
Grado della sorgente di emissione: SECONDO
-
Disponibilità della ventilazione: ADEGUATA19
-
Grado della diluzione: MEDIO
-
si ottiene una zona di tipo 2 IIAT1 estesa.
Tabella 12.8 – Matrice di classificazione (cfr. Allegato D, EN IEC 60079-10-1:2021)13
| Grado di emissione | Efficacia della ventilazione | ||||||
|---|---|---|---|---|---|---|---|
| Diluizione Alta | Diluizione Media | Diluizione Bassa | |||||
| Disponibilità della ventilazione | |||||||
| Buona | Adeguata | Scarsa | Buona | Adeguata | Scarsa | Buona, adeguata o scarsa | |
| Continuo | Non hazardous [Zona 0NE]1 | Zona 2 [Zona 0NE]1 | Zona 1 [Zona 0NE]1 | Zona 0 | Zona 0 + Zona 23 | Zona 0 + Zona 1 | Zona 0 |
| Primo | Non hazardous [Zona 1NE]1 | Zona 2 [Zona 1NE]1 | Zona 2 [Zona 1NE] | Zona 1 | Zona 1 + Zona 2 | Zona 1 + Zona 2 | Zona 1 oppure Zona 04 |
| Secondo2 | Non hazardous [Zona 2NE]1 | Non hazardous [Zona 2NE]1 | Zona 2 | Zona 2 | Zona 2 IIAT1 | Zona 2 | Zona 1 e persino Zona 04 |
A titolo di confronto si utilizza ora l’equazione f.GB.5.1-5a, ex CEI 31-35:2012 che fornisce valori affidabili e riproducibili in presenza di equilibrio termico tra lo stoccaggio del gas pressurizzato e la temperatura ambiente. Si ha:
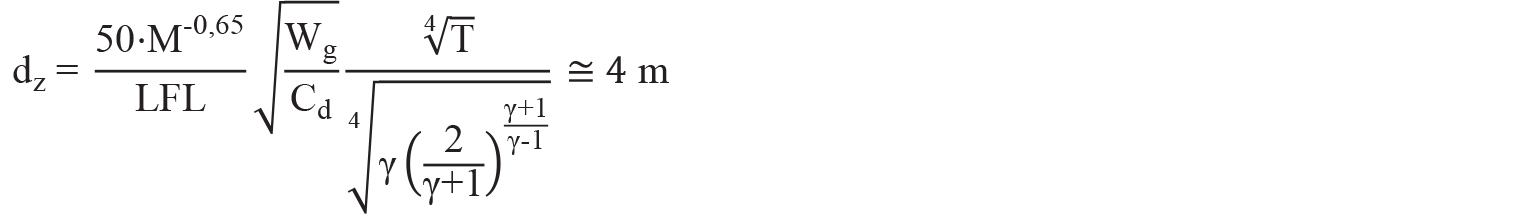
Risultato in svantaggio di sicurezza rispetto a quello ottenuto con l’equazione NFPA 2:2023. L’equazione presente in ex CEI 31-35:2012, seppur estremamente affidabile in ambiti di rilascio convenzionali, entra in crisi in situazione di rilevante differenza termica tra interno ed esterno del contenimento.
Commento: i risultati del calcolo svolto con il software ingegneristico HyRAM+ v5.0 di
SANDIA (USA) è il seguente:
-
Maximum mass flow rate [kg/s]: 1,460E-001
-
Maximum distance to flammable concentration [m]: 4 ÷ 5,1 m
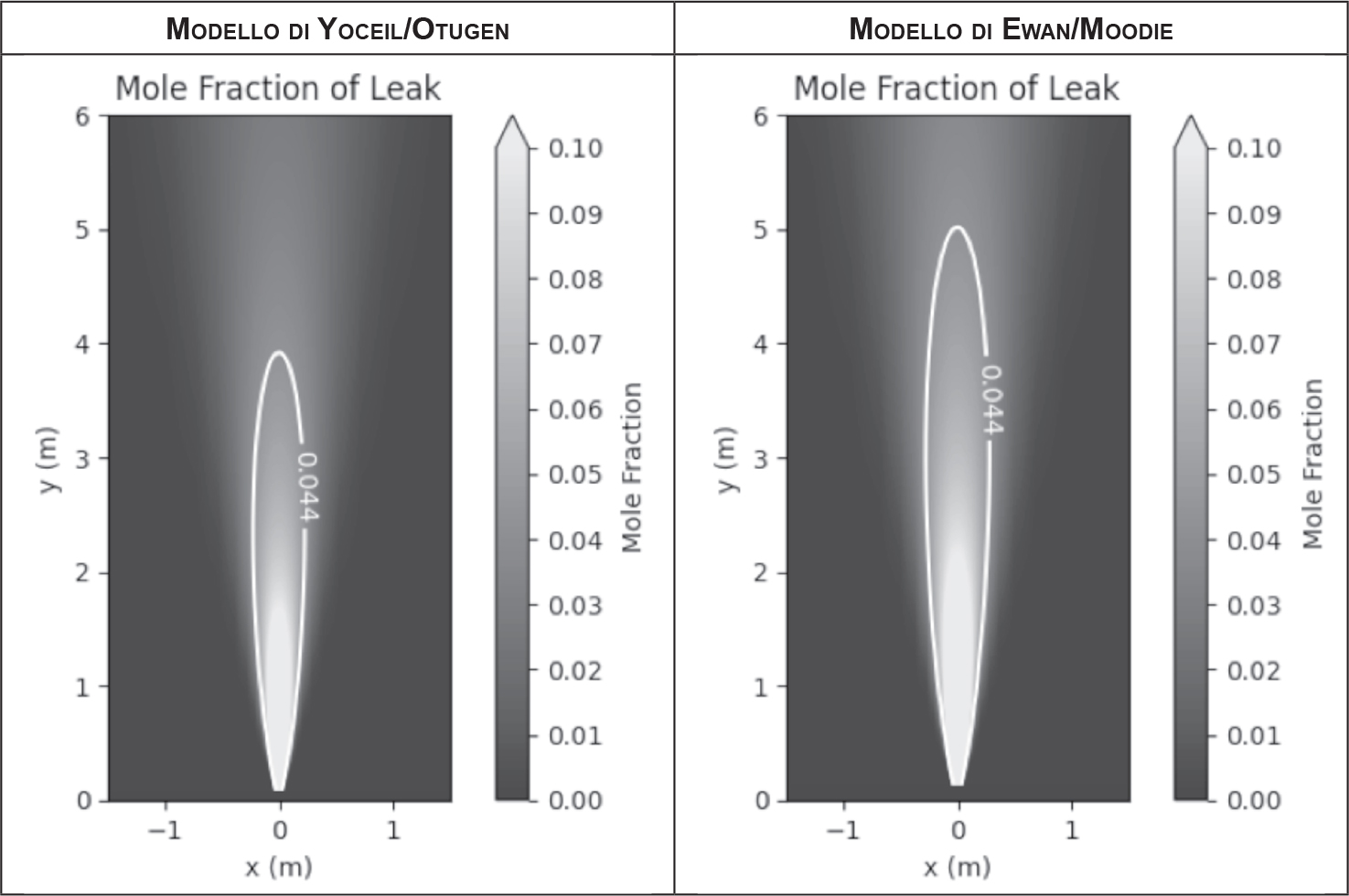
Dove la distanza minima del range è calcolata con il modello Yoceil/Otugen e la massima è calcolata con il modello di Ewan/Moodie.
Figura 12.19 – Range delle distanze calcolate dal SW HyRAM+ v5.0 di SANDIA
La determinazione della distanza pericolosa fatta invece in base al nomogramma dell’Allegato D, CEI EN IEC 60079-10-1:2021 è di seguito riportata.
Figura 12.20 – Determinazione della distanza pericolosa (cfr. Allegato D, EN IEC 60079-10-1:2021)
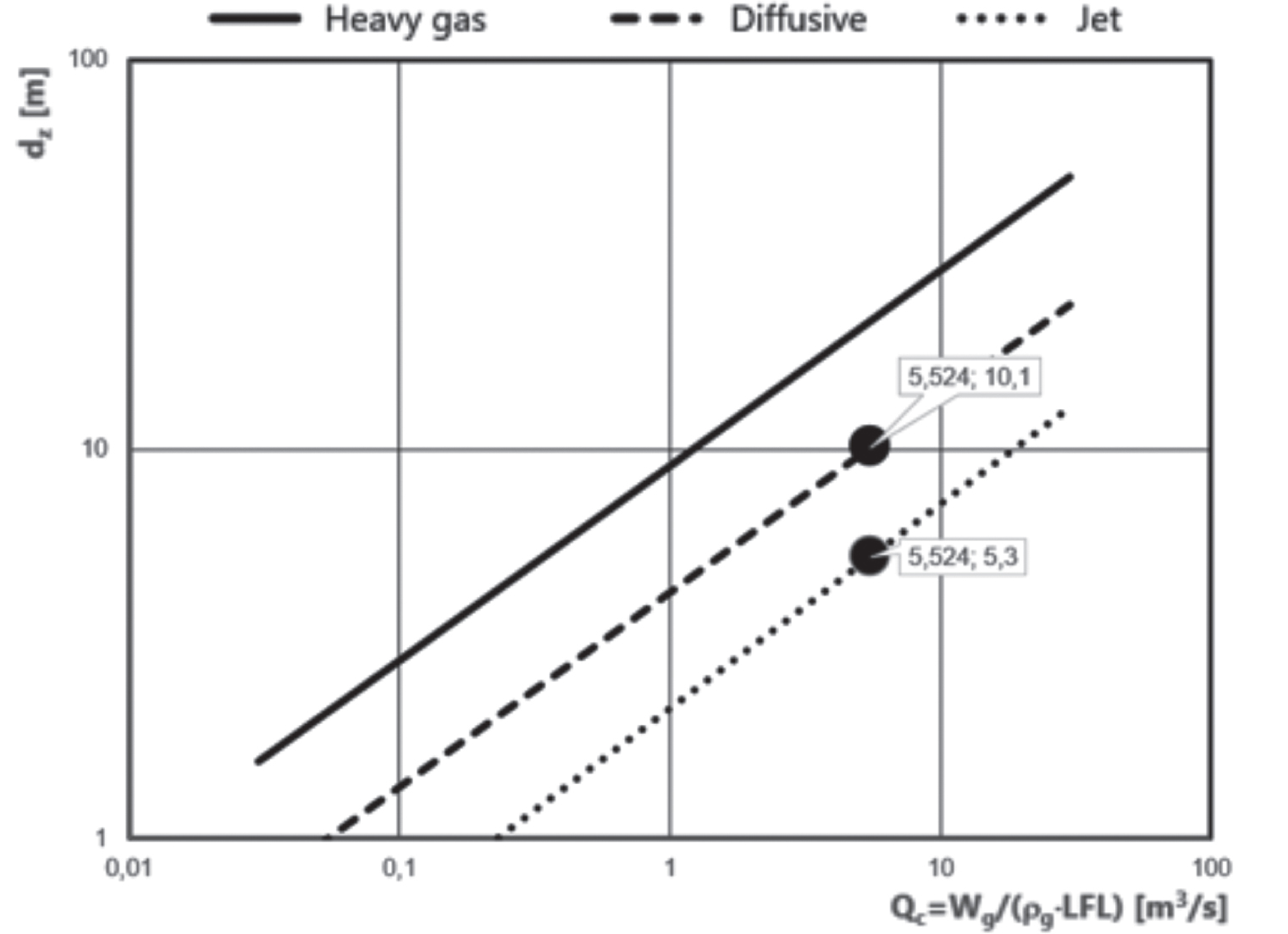
La dz è quindi pari a 5,3 m per rilascio a getto mentre risulta di ampiezza uguale a 10,1 m per dispersione diffusiva/passiva.
La dz,NFPA2 sembra essere il modello maggiormente aderente agli attuali standard tecnici di riferimento (IL software HyRAM+ v5.0 di SANDIA, con il quale il valore calcolato è in accordo, è citato, quale “gold standard”, in UNI ISO 19880-1:2020): assumiamo definitivamente che la distanza a rischio di esplosione sia quella calcolata con il modello NFPA 2:2023. Si ha:
r = dz = dz,NFPA2 = 4,5 m
Poiché la direzione di rilascio è nota, la forma sarà quella di un cono (a rovescio) con diametro di base, assumendo un angolo di emissione di circa 30° + 30° (cfr. art. 5.11.2.3, ex CEI 31-35:2012), pari a circa:
r” = 2,6 m.
Infine, per la definizione di r’ si farà ricorso alla seguente equazione empirica:

La forma della zona classificata possiede, in conclusione, le seguenti caratteristiche:
-
Estensione verticale superiore, dz = r = 4,5 m a partire dalla sorgente di emissione
-
Diametro di base del cono, 2r” = 5,2 m
-
Estensione verticale inferiore, r’ = 0,3 m
-
Forma: conica (Fonte: IEC, 2021)
Figura 12.21 – Forma della zona classificata
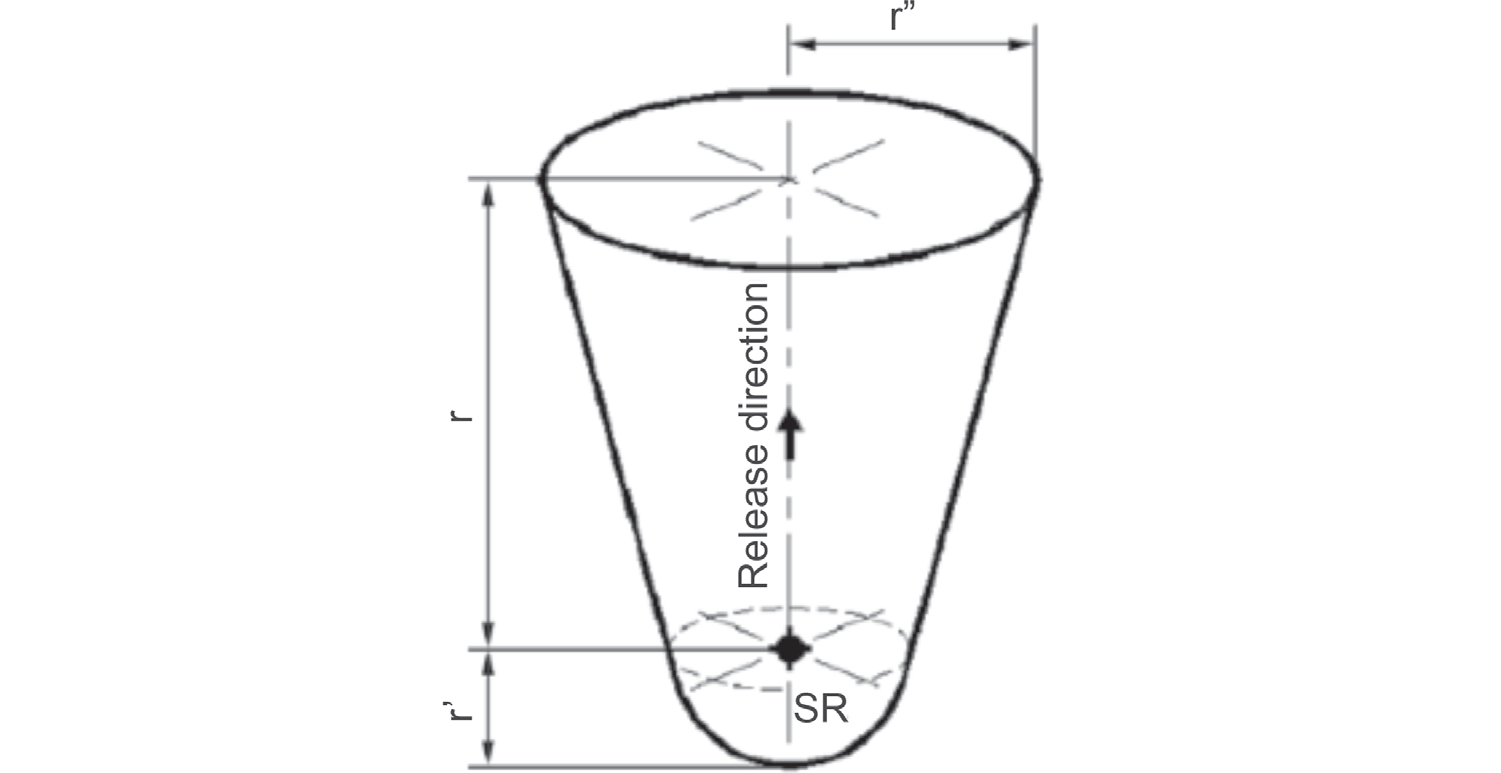
Fonte: IEC, 2021
Note a piè di pagina
-
Le zone 0NE, 1NE oppure 2NE indicano zone teoriche le quali, sotto normali condizioni, possiedono estensione trascurabile.
-
L’area di una zona 2 generata da una sorgente di emissione di secondo grado può superare quella riferibile ad una sorgente di emissione di grado primo o continuo; in queste circostanze deve essere assunta la maggiore distanza.
-
La zona 1 non è necessaria in questo caso. In altre parole, una piccola Zona 0 si trova nell’area in cui il rilascio non è controllato dalla ventilazione e una Zona 2 più grande per quando la ventilazione non funziona.
-
Sarà zona 0 se la ventilazione è così debole e il rilascio è tale che in pratica l’ATEX esiste praticamente in modo ininterrotto (condizioni di “assenza di ventilazione”).